题目内容
 如图,点A、B、C、D在同一个圆上,DB=DC,DA、CB的延长线相交于点E.若∠BDC=α,则∠EAB=
如图,点A、B、C、D在同一个圆上,DB=DC,DA、CB的延长线相交于点E.若∠BDC=α,则∠EAB=考点:圆内接四边形的性质
专题:
分析:先根据等腰三角形的性质求出∠C的度数,再由圆内接四边形的性质即可得出结论.
解答:解:∵DB=DC,∠BDC=α,
∴∠C=
=90°-
α.
∵四边形ABCD内接是圆内接四边形,、
∴∠EAB=∠C=90°-
α.
故答案为:90°-
α.
∴∠C=
| 180°-α |
| 2 |
| 1 |
| 2 |
∵四边形ABCD内接是圆内接四边形,、
∴∠EAB=∠C=90°-
| 1 |
| 2 |
故答案为:90°-
| 1 |
| 2 |
点评:本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
相关题目
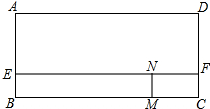 如图,已知矩形ABCD,AB=6cm,BC=8cm,E、F分别是AB、CD上的点,且AE=DF=4cm,两动点M、N分别从C、F两点同时出发沿CB、FE均以2cm/s的速度向B、E两点运动,猜测当M、N运动多长时间,矩形CFNM与矩形AEFD相似?写出你的猜测过程,与同学交流.
如图,已知矩形ABCD,AB=6cm,BC=8cm,E、F分别是AB、CD上的点,且AE=DF=4cm,两动点M、N分别从C、F两点同时出发沿CB、FE均以2cm/s的速度向B、E两点运动,猜测当M、N运动多长时间,矩形CFNM与矩形AEFD相似?写出你的猜测过程,与同学交流.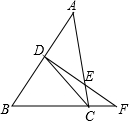 如图,已知CD是直角△ABC斜边上的中线,DF交AC于E,交BC延长线于F,且CD2=DE•DF,求证:
如图,已知CD是直角△ABC斜边上的中线,DF交AC于E,交BC延长线于F,且CD2=DE•DF,求证: 已知CE∥DF,∠ABF=100°,∠CAB=20°,则∠ACE的度数为多少度?
已知CE∥DF,∠ABF=100°,∠CAB=20°,则∠ACE的度数为多少度? 某小区规划在边长为x米的正方形场地修建两条宽两米的小路,如图,其余部分种草,求草地面积.
某小区规划在边长为x米的正方形场地修建两条宽两米的小路,如图,其余部分种草,求草地面积.