题目内容
8.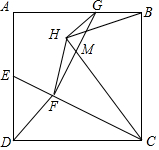 如图,正方形ABCD中,AB=4,E为AD中点,连接CE,F为CE上一点,且CF=$\sqrt{5}$+1,过点F作FG⊥CE交AB于G,连接DF,将△CDF沿着CE翻折得到△CHF,CH与FG相交于M,连接GH,则四边形CHGB的面积为5+$\frac{\sqrt{5}}{5}$.
如图,正方形ABCD中,AB=4,E为AD中点,连接CE,F为CE上一点,且CF=$\sqrt{5}$+1,过点F作FG⊥CE交AB于G,连接DF,将△CDF沿着CE翻折得到△CHF,CH与FG相交于M,连接GH,则四边形CHGB的面积为5+$\frac{\sqrt{5}}{5}$.
分析 如图,作KL⊥AD于L,HN⊥AB于N,延长FG交CB的延长线于P,连接AH、EH、DH,EC与DH交于点K.首先证明△AHD是直角三角形,EK是△ADH的中位线,根据四边形CHGB的面积=正方形ABCD的面积-四边形DEHC的面积-△AHE的面积-△AHG的面积,求出相关线段即可解决问题.
解答 解:如图,作KL⊥AD于L,HN⊥AB于N,延长FG交CB的延长线于P,连接AH、EH、DH,EC与DH交于点K.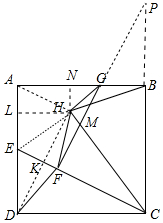
∵四边形ABCD是正方形,
∴∠ADC=∠ABC=∠PBG=90°,
在Rt△DEC中,EC=$\sqrt{C{D}^{2}+D{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∵△HCF是由△FCD翻折得到,
∴DE=EH=AE,EC⊥DH,
∴∠AHD=90°
∵$\frac{1}{2}$•DE•DC=$\frac{1}{2}$•EC•DK,
∴DK=KH=$\frac{4}{\sqrt{5}}$,
在Rt△DEK中,EK=$\sqrt{D{E}^{2}-D{K}^{2}}$=$\frac{2}{\sqrt{5}}$,
∵AE=DE,DK=HK,
∴AH=2EK=$\frac{4}{\sqrt{5}}$,
∵∠HAL=∠DAH,∠ALH=∠AHD,
∴△ALH∽△AHD,
∴AH2=AL•AD,
∴AL=HN=$\frac{A{H}^{2}}{AD}$=$\frac{4}{5}$,
在Rt△ALH中,HL=$\sqrt{A{H}^{2}-A{L}^{2}}$=$\frac{8}{5}$,
∵△DCE∽△FPC∽△BPG,
∴$\frac{DE}{CD}$=$\frac{CF}{PF}$=$\frac{BG}{PB}$=$\frac{1}{2}$,
∵CF=1+$\sqrt{5}$,
∴PF=2+2$\sqrt{5}$,
PC=$\sqrt{5}$CF=5+$\sqrt{5}$,
∴PB=PC-BC=1+$\sqrt{5}$,
∴BG=$\frac{1+\sqrt{5}}{2}$,AG=AB-BG=$\frac{7-\sqrt{5}}{2}$,
∴四边形CHGB的面积=正方形ABCD的面积-四边形DEHC的面积-△AHE的面积-△AHG的面积
=16-2•$\frac{1}{2}$•4•2-$\frac{1}{2}$•2•$\frac{8}{5}$-$\frac{1}{2}$$\frac{7-\sqrt{5}}{2}$•$\frac{4}{5}$=5+$\frac{\sqrt{5}}{5}$.
故答案为5+$\frac{\sqrt{5}}{5}$.
点评 本题考查翻折变换、正方形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会利用分割法求面积,是由中考填空题中的压轴题.

| A. | 1600名学生 | |
| B. | 100名学生 | |
| C. | 所抽取的100名学生对“红军长征历史”的知晓情况 | |
| D. | 每一名学生对“红军长征历史”的知晓情况 |
 如图,在△ABC中,AB=AC,∠A=40°,以C为圆心,CB的长为半径画弧,交AB于点D,连接CD,则∠ACD等于( )
如图,在△ABC中,AB=AC,∠A=40°,以C为圆心,CB的长为半径画弧,交AB于点D,连接CD,则∠ACD等于( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |