题目内容
数轴上两定点A、B对应的数分别是-18和14,现在有甲、乙两只电子蚂蚁分别从A、B两点同时出发,沿着数轴爬行,速度分别为每秒1.5个单位和1.7个单位.它们第一次相向爬行1秒,第二次反向爬行2秒,第三次相向爬行3秒,第四次反向爬行4秒,第五次相向爬行5秒…,按如此规律,则它们第一次相遇时所需的时间为多少秒?
考点:数轴
专题:规律型
分析:根据两点间的距离,可得BA的长,根据爬行的规律,可得以后每两次可以前进3.2,可得爬行的总次数,根据有理数的加法,可得答案.
解答:解:AB之间的距离为14-(-18)=32,
第一次相向爬行1秒后,两只蚂蚁相距32-1×(1.5+1.7)=28.8,
以后每两次可以前进3.2,
∴28.8÷3.2=9,
则最后一次是第19次,即甲乙两只电子蚂蚁相向爬行19秒,
故第一次相遇的时间为1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19=(1+19)19÷2=190(秒),
答:它们第一次相遇时所需的时间为190秒.
第一次相向爬行1秒后,两只蚂蚁相距32-1×(1.5+1.7)=28.8,
以后每两次可以前进3.2,
∴28.8÷3.2=9,
则最后一次是第19次,即甲乙两只电子蚂蚁相向爬行19秒,
故第一次相遇的时间为1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19=(1+19)19÷2=190(秒),
答:它们第一次相遇时所需的时间为190秒.
点评:本题考查了数轴,根据爬行的规律得出前进的速度,爬行的总次数是解题关键.

练习册系列答案
相关题目
 如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,AD=AE
如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,AD=AE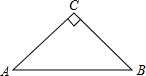 如图,△ABC是等腰Rt三角形,∠C=90°,AC=4.
如图,△ABC是等腰Rt三角形,∠C=90°,AC=4.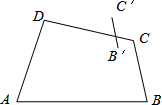 如图所示,已知四边形ABCD和线段B′C′,且线段BC与线段B′C′是位似图形.
如图所示,已知四边形ABCD和线段B′C′,且线段BC与线段B′C′是位似图形.