题目内容
16.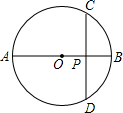 如图:⊙O的直径AB=10,CD是⊙O的弦,且CD⊥AB于P,已知BP:AP=1:4,则CD的长为( )
如图:⊙O的直径AB=10,CD是⊙O的弦,且CD⊥AB于P,已知BP:AP=1:4,则CD的长为( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
分析 连接OC,由于AB是⊙O的直径,弦CD⊥AB于点P,所以CD=2CP,再由AB=10,BP:AP=1:4,可求出OC及OP的长,在Rt△CPO中利用勾股定理可求出CP的长,故可得出结论.
解答 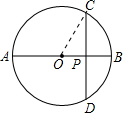 解:连接OC,
解:连接OC,
∵AB是⊙O的直径,弦CD⊥AB于P,
∴CD=2CP,
∵AB=10,BP:AP=1:4,
∴OC=OB=5,BP=2,AP=8,
∴OP=OB-BP=3,
在Rt△C,PO中,CP=$\sqrt{O{C}^{2}-O{P}^{2}}$=4,
∴CD=8.
故选B.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.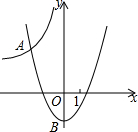 如图,二次函数y=x2+bx+c的图象过点B(0,-2),它与反比例函数y=-$\frac{8}{x}$的图象交于点A(m,4),则这二次函数图象的对称轴是( )
如图,二次函数y=x2+bx+c的图象过点B(0,-2),它与反比例函数y=-$\frac{8}{x}$的图象交于点A(m,4),则这二次函数图象的对称轴是( )
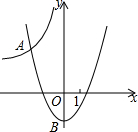 如图,二次函数y=x2+bx+c的图象过点B(0,-2),它与反比例函数y=-$\frac{8}{x}$的图象交于点A(m,4),则这二次函数图象的对称轴是( )
如图,二次函数y=x2+bx+c的图象过点B(0,-2),它与反比例函数y=-$\frac{8}{x}$的图象交于点A(m,4),则这二次函数图象的对称轴是( )| A. | 直线x=$\frac{1}{4}$ | B. | 直线x=$\frac{1}{3}$ | C. | 直线x=$\frac{1}{2}$ | D. | 直线x=$\frac{2}{3}$ |
8.不等式2x-5≤0的非整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
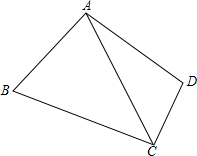 如图所示四边形ABCD,AB=AD,∠BAD=∠BCD=90°,SABCD=24cm2,求AC的长.
如图所示四边形ABCD,AB=AD,∠BAD=∠BCD=90°,SABCD=24cm2,求AC的长.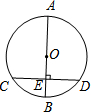 如图,AB是⊙O的直径,弦CD⊥AB于E,CE=3,则CD的长度是6.
如图,AB是⊙O的直径,弦CD⊥AB于E,CE=3,则CD的长度是6.