题目内容
4.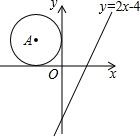 如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x-4上,则⊙A的半径为( )
如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x-4上,则⊙A的半径为( )| A. | $\frac{4}{3}$ | B. | 2 | C. | 4 | D. | 6 |
分析 由切线的性质可设A点的坐标为(a,-a),再由平移可得到平移后的圆心坐标,代入直线解析式可求得a的值,可得出答案.
解答  解:
解:
过A分别作x轴、y轴的垂线,垂足分别为E、F,如图,
∵⊙A与x轴、y轴相切,
∴AE=AF,
∵A在第二象限,
∴可设A点坐标为(a,-a),
又A点向右平移5个单位,
∴A点平移后的坐标为(a+5,-a),
此时A点坐标在直线y=2x-4上,
∴-a=2(a+5)-4,解得a=-2,
∴AF=2,即⊙A的半径为2,
故选B.
点评 本题主要考查切线的性质及平移的性质,用A点坐标表示出平移后的坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.二次函数y=x2-|k|与正比例函数y=kx(k≠0)图象的位置关系为( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |
13.下列实数中是无理数的是( )
| A. | $\sqrt{4}$ | B. | $\root{3}{8}$ | C. | π0 | D. | sin45° |
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.
 如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )