题目内容
9.先化简,再求值:$\frac{{{a^2}+2ab+{b^2}}}{{{a^2}-{b^2}}}-\frac{a}{a-b}$,其中a=3,b=2.分析 原式第一项约分后,利用同分母分式的减法法则计算得到最简结果,把a与b的值代入计算即可求出值.
解答 解:原式=$\frac{(a+b)^{2}}{(a+b)(a-b)}$-$\frac{a}{a-b}$=$\frac{a+b-a}{a-b}$=$\frac{b}{a-b}$,
当a=3,b=2时,原式=$\frac{2}{3-2}$=2.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
17.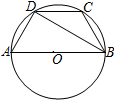 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )| A. | 25πcm2 | B. | 49πcm2 | C. | 32πcm2 | D. | 36πcm2 |
4.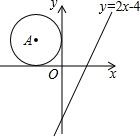 如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x-4上,则⊙A的半径为( )
如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x-4上,则⊙A的半径为( )
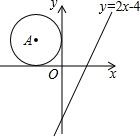 如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x-4上,则⊙A的半径为( )
如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x-4上,则⊙A的半径为( )| A. | $\frac{4}{3}$ | B. | 2 | C. | 4 | D. | 6 |
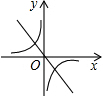
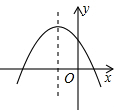 二次函数y=ax2+bx+c的图象如图,则函数y=$\frac{a}{x}$与函数y=bx在同一坐标系内的大致图象是( )
二次函数y=ax2+bx+c的图象如图,则函数y=$\frac{a}{x}$与函数y=bx在同一坐标系内的大致图象是( )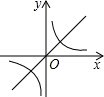

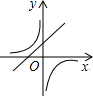
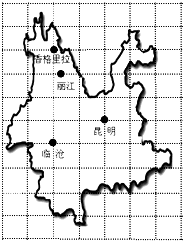 北京二中组织同学去云南省春游,在地图上设定的临沧市位置点的坐标为(-1,0),出发点昆明市位置点的坐标为(1,1).如图请帮助小强确定出终点香格里拉位置点的坐标为(-1,4).
北京二中组织同学去云南省春游,在地图上设定的临沧市位置点的坐标为(-1,0),出发点昆明市位置点的坐标为(1,1).如图请帮助小强确定出终点香格里拉位置点的坐标为(-1,4).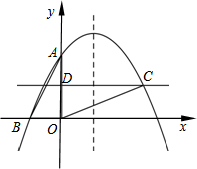 如图,在平面直角坐标系中,一条抛物线经过点A(0,2)、B(-1,0),且对称轴为直线x=1.点C是抛物线上x轴上方任意一点,直线CD平行于x轴,与y轴交于点D.设点C的横坐标为x.
如图,在平面直角坐标系中,一条抛物线经过点A(0,2)、B(-1,0),且对称轴为直线x=1.点C是抛物线上x轴上方任意一点,直线CD平行于x轴,与y轴交于点D.设点C的横坐标为x.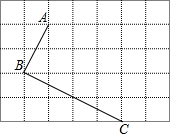 如图,在方格纸中,每个小方格的边长为1,把线段AB沿BC方向平移BC的长度后,线段AB所扫过的面积是10.
如图,在方格纸中,每个小方格的边长为1,把线段AB沿BC方向平移BC的长度后,线段AB所扫过的面积是10.