题目内容
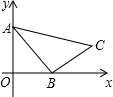 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=| 3 |
考点:勾股定理,坐标与图形性质,三角形三边关系,直角三角形斜边上的中线
专题:
分析:连接OC,交AB于点E,过点C作CF⊥x轴于点F,E为AB的中点,当O,E及C共线时,OC最大,此时OE=
AB=1,由勾股定理求出CE=2,OC=3,设C的坐标是(x,y),由勾股定理得:x2+y2=32,再证明△AOB∽△EBC,△AOB∽△CEO,可得:
=
,
=
,再代入相应的数值可得:
x=y,x2+y2=32即可得出结论.
| 1 |
| 2 |
| AB |
| CO |
| BO |
| EO |
| BO |
| EO |
| AB |
| BC |
| ||
| 3 |
解答: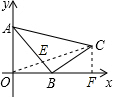 解:连接OC,交AB于点E,点C作CF⊥x轴于点F,E为AB的中点,当O,E及C共线时,OC最大,
解:连接OC,交AB于点E,点C作CF⊥x轴于点F,E为AB的中点,当O,E及C共线时,OC最大,
此时OE=BE=
AB=1,由勾股定理得:CE=
=2,
OC=1+2=3,
设C的坐标是(x,y),
由勾股定理得:x2+y2=32,
∵EO=BE,
∴∠EOB=∠EBO,
∵∠CFO=∠AOB=90°,∠EOB=∠EBO,
∴△AOB∽△CFO,
∴
=
,
∴
=
,
∴OB=
x,
∵∠CBA=90°,CE=2,BE=1,
∴∠BCO=30°,∠CEB=60°,
∴∠AEO=∠CEB=60°,
∵AE=OE,
∴△AEO是等边三角形,
∴∠BAO=∠CEB=60°,∠CBE=∠AOB=90°,
∵△AOB∽△EBC,
∴
=
,
∴
=
,
∴
=
,
∴
x=y,
∴x2+(
x)2=32,
解得:x=
,y=
.
故答案为:(
,
).
 解:连接OC,交AB于点E,点C作CF⊥x轴于点F,E为AB的中点,当O,E及C共线时,OC最大,
解:连接OC,交AB于点E,点C作CF⊥x轴于点F,E为AB的中点,当O,E及C共线时,OC最大,此时OE=BE=
| 1 |
| 2 |
| BC2+BE2 |
OC=1+2=3,
设C的坐标是(x,y),
由勾股定理得:x2+y2=32,
∵EO=BE,
∴∠EOB=∠EBO,
∵∠CFO=∠AOB=90°,∠EOB=∠EBO,
∴△AOB∽△CFO,
∴
| AB |
| CO |
| BO |
| FO |
∴
| 2 |
| 3 |
| BO |
| x |
∴OB=
| 2 |
| 3 |
∵∠CBA=90°,CE=2,BE=1,
∴∠BCO=30°,∠CEB=60°,
∴∠AEO=∠CEB=60°,
∵AE=OE,
∴△AEO是等边三角形,
∴∠BAO=∠CEB=60°,∠CBE=∠AOB=90°,
∵△AOB∽△EBC,
∴
| BO |
| CE |
| AB |
| BC |
∴
| BO |
| y |
| 2 | ||
|
∴
| ||
| y |
| 2 | ||
|
∴
| ||
| 3 |
∴x2+(
| ||
| 3 |
解得:x=
3
| ||
| 2 |
| 3 |
| 2 |
故答案为:(
3
| ||
| 2 |
| 3 |
| 2 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
如果|x|+x=0,那么x应为( )
| A、负数 | B、负数或零 |
| C、正数 | D、正数或零 |
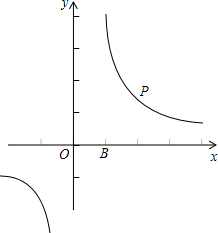 如图,点P是函数y=
如图,点P是函数y= 已知AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠ABO=32°,则∠AOC=
已知AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠ABO=32°,则∠AOC= 如图,用3个边长为1的正方形组成一个对称图形,则能将其完全覆盖的圆的最小半径为
如图,用3个边长为1的正方形组成一个对称图形,则能将其完全覆盖的圆的最小半径为 如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A出发向南偏西15°方向走30m至点C,则∠BAC的度数是
如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A出发向南偏西15°方向走30m至点C,则∠BAC的度数是