题目内容
18.已知实数x、y满足x2+x+y-1=0,则y-x的最大值为2.分析 先把x2+x+y-1=0变形得到y=-x2-x+1,再代入y-x,利用二次函数的性质求值.
解答 解:∵x2+x+y-1=0,
∴
∴y-x=-x2-x+1-x═-x2-2x+1,
∵a=-1>0,
∴当x=$-\frac{b}{2a}$=$-\frac{-2}{-1×2}$=-1时,y-x有最大值$\frac{4×(-1)×1{-(-2)}^{2}}{4×(-1)}$=2,
故答案为:2.
点评 本题考查了二次函数的最值,把求代数式的最大值转化为求函数的最大值,把代数式和二次函数结合起来是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.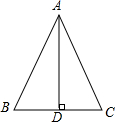 如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )
如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )
 如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )
如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )| A. | ASA | B. | SAS | C. | SSS | D. | HL |
7.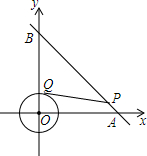 如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
 如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )| A. | 3 | B. | 2 | C. | 3-$\sqrt{2}$ | D. | 2 $\sqrt{2}$ |
 如图∠ABC=∠CDB=90°,AC∥BD.
如图∠ABC=∠CDB=90°,AC∥BD.