题目内容
19. 如图,H、L是平行四边形ABCD对角线AC上两点,BH∥DL,求证:AL=CH.
如图,H、L是平行四边形ABCD对角线AC上两点,BH∥DL,求证:AL=CH.
分析 由平行四边形的性质得出AD=CB,AD∥CB,得出∠DAL=∠BCH,由平行线的性质得出∠ALD=∠CHB,由AAS证明△ADL≌△CBH,得出对应边相等即可.
解答 证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB,
∴∠DAL=∠BCH,
∵BH∥DL,
∴∠ALD=∠CHB,
在△ADL和△CBH中,
$\left\{\begin{array}{l}{∠DAL=∠BCH}&{\;}\\{∠ALD=∠CHB}&{\;}\\{AD=CB}&{\;}\end{array}\right.$,
∴△ADL≌△CBH(AAS),
∴AL=CH.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、平行线的性质;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
10.在中国旅游日(5月19日),我市旅游部门对2011年第一季度游客在湖州的旅游时间作抽样调查,统计如下:
若将统计情况制成扇形统计图,则表示旅游时间为“2~3天”的扇形圆心角的度数为( )
| 旅游时间 | 当天往返 | 2~3天 | 4~7天 | 8~14天 | 半月以上 | 合计 |
| 人数(人) | 76 | 120 | 80 | 19 | 5 | 300 |
| A. | 216° | B. | 144° | C. | 72° | D. | 36° |
9.张强在九年级的六次数学测试中成绩如下(单位:分):76,89,91,85,84,85,则这六次测试成绩的平均数、中位数和众数分别为( )
| A. | 85,88,84 | B. | 84,88,85 | C. | 85,85,85 | D. | 86,84.5,85 |
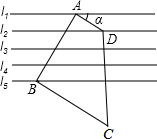 如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离都相等,如果直角梯形ABCD的三个顶点在平行直线上,∠ABC=90°且AB=3AD,则sinα=$\frac{3}{5}$.
如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离都相等,如果直角梯形ABCD的三个顶点在平行直线上,∠ABC=90°且AB=3AD,则sinα=$\frac{3}{5}$. 如图,AB∥CD,∠B=52°,∠D=18°,则∠E的度数为34°.
如图,AB∥CD,∠B=52°,∠D=18°,则∠E的度数为34°.