题目内容
1．如果等腰三角形的周长为27，一边长为13，那么腰长为7或13．分析 题中给出了周长和一边长，而没有指明这边是否为腰长，则应该分两种情况进行分析求解．
解答 解：①当13为腰长时，则腰长为13，底边=27-13-13=1，因为13+1＞13，所以能构成三角形；
②当13为底边时，则腰长=（27-13）÷2=7，因为7+7＞13，所以能构成三角形．
故答案为：7或13．
点评 此题主要考查等腰三角形的性质及三角形三边关系的综合运用，关键是利用三角形三边关系进行检验．
练习册系列答案
相关题目
12．下列命题中，真命题是（ ）
| A． | 对角线相等的四边形是矩形 | |
| B． | 对角线互相垂直的四边形是菱形 | |
| C． | 两条对角线互相平分且相等的四边形是正方形 | |
| D． | 顺次连接四边形的各边中点所得的四边形是平行四边形 |
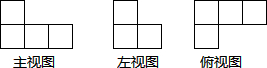在一个仓库里堆放有若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画出来，如图，则这堆货箱共有5个．
6．化简$\sqrt{8{a}^{2}}$的结果是（ ）
| A． | 4a$\sqrt{2}$ | B． | 16$\sqrt{{a}^{2}}$ | C． | 2a$\sqrt{4}$ | D． | 2a$\sqrt{2}$ |
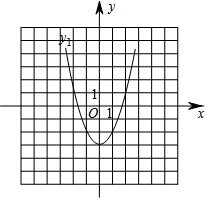如图为抛物线y1=x2-3，且抛物线y2是由抛物线y1向右平移2个单位得到的．
如图，⊙O为锐角三角形ABC的外接圆，若∠BAO=18°，则∠C的度数为72°．