题目内容
 如图,Rt△ABC中,D是AB上一点,BD=BC,过D作AB的垂线交AC于点E,CD交BE于点F
如图,Rt△ABC中,D是AB上一点,BD=BC,过D作AB的垂线交AC于点E,CD交BE于点F①∠A=40°,求∠CDB的度数;
②求证:BE垂直平分CD.
考点:线段垂直平分线的性质
专题:
分析:①由题意可知D为AB的中点,由直角三角形的性质可知DC=DA,再结合三角形外角的性质可求得∠CDB=2∠A,可求得∠CDB;
②由条件可证明△BCE≌△BDE,可得EC=ED,可得BE为CD的垂直平分线.
②由条件可证明△BCE≌△BDE,可得EC=ED,可得BE为CD的垂直平分线.
解答:①解:∵DE为AB的垂直平分线,
∴D为AB中点,
∵∠ACB=90°,
∴DC=DA,
∴∠ACD=∠A=40°,
∴∠CDB=2∠A=80°;
②证明:在Rt△BCE和Rt△BDE中,
∴Rt△BCE≌Rt△BDE(HL),
∴EC=ED,
∴点B和点E在线段CD的垂直平分线上,
∴BE垂直平分CD.
∴D为AB中点,
∵∠ACB=90°,
∴DC=DA,
∴∠ACD=∠A=40°,
∴∠CDB=2∠A=80°;
②证明:在Rt△BCE和Rt△BDE中,
|
∴Rt△BCE≌Rt△BDE(HL),
∴EC=ED,
∴点B和点E在线段CD的垂直平分线上,
∴BE垂直平分CD.
点评:本题主要考查线段垂直平分线的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,几何体的主视图是( )
如图,几何体的主视图是( )A、 |
B、 |
C、 |
D、 |
△ABO的顶点坐标分别是A(-3,3)、B(3,3)、O(0,0),试将△ABO放大,使△ABO与△EFO的位似比为1:2,则点E和点F的坐标可能分别为( )
| A、(-6,6),(6,6) |
| B、(6,-6),(6,6) |
| C、(-6,6),(6,-6) |
| D、(6,6),(-6,-6) |
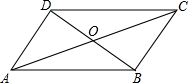 如图,在?ABCD中,对角线AC,BD相交于点O,AD=3
如图,在?ABCD中,对角线AC,BD相交于点O,AD=3
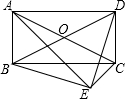 已知:如图,在四边形ABCD中,以AC为斜边作Rt△ACE,且∠BED为直角.求证:四边形ABCD是矩形.
已知:如图,在四边形ABCD中,以AC为斜边作Rt△ACE,且∠BED为直角.求证:四边形ABCD是矩形. 明月兔业养殖厂在兔舍外面开辟一个面积为20平方米的长方形活动场地,准备一边靠墙,其余三边利用长14米的旧围栏,已知兔舍墙面宽6米,问围成长方形的长和宽各是多少米?
明月兔业养殖厂在兔舍外面开辟一个面积为20平方米的长方形活动场地,准备一边靠墙,其余三边利用长14米的旧围栏,已知兔舍墙面宽6米,问围成长方形的长和宽各是多少米?