题目内容
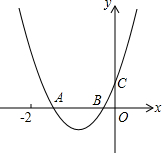 如图,二次函数y=ax2+bx+c的图象与X轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2,②b2-4ac<4a2,③a>1,其中正确的个数为( )
如图,二次函数y=ax2+bx+c的图象与X轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2,②b2-4ac<4a2,③a>1,其中正确的个数为( )| A、0个 | B、1个 | C、2个 | D、3个 |
考点:二次函数图象与系数的关系
专题:
分析:由根与系数的关系及二次函数y=ax2+bx+c的图象坐标逐一求判定即可.
解答:解:①∵OB=OC,
∴C(0,c),B(-c,0)
把B(-c,0)代入y=ax2+bx+c得0=ac2-bc+c,即0=ac2+c(1-b),
∵a>0,
∴1-b<0,即b>1,
如果b=2,由0=ac2-bc+c,可得ac=1,此是△=b2-4ac=0,故b>1且b≠2正确,
②∵a>0,b>0,c>0,设C(0,c),B(-c,0)
∵AB=|x1-x2|<2,
∴(x1+x2)2-4x1x2<4,
∴(-
)2-4×
<4,即
-
<4,
∴b2-4ac<4a2;故本项正确.
③把B(-c,0)代入y=ax2+bx+c可得ac+1=b,
代入y=ax2+bx+c得y=ax2+(ac+1)x+c=ax2+acx+x+c=ax2+x+acx+c=x(ax+1)+c(ax+1)=(x+c)(ax+1),
解得x1=-c,x2=-
,
由图可得x2>-1,
即-
>-1,
∵a>0,
∴a>1;正确.
所以正确的个数是3个.
故选D.
∴C(0,c),B(-c,0)
把B(-c,0)代入y=ax2+bx+c得0=ac2-bc+c,即0=ac2+c(1-b),
∵a>0,
∴1-b<0,即b>1,
如果b=2,由0=ac2-bc+c,可得ac=1,此是△=b2-4ac=0,故b>1且b≠2正确,
②∵a>0,b>0,c>0,设C(0,c),B(-c,0)
∵AB=|x1-x2|<2,
∴(x1+x2)2-4x1x2<4,
∴(-
| b |
| a |
| c |
| a |
| b2 |
| a2 |
| 4c |
| a |
∴b2-4ac<4a2;故本项正确.
③把B(-c,0)代入y=ax2+bx+c可得ac+1=b,
代入y=ax2+bx+c得y=ax2+(ac+1)x+c=ax2+acx+x+c=ax2+x+acx+c=x(ax+1)+c(ax+1)=(x+c)(ax+1),
解得x1=-c,x2=-
| 1 |
| a |
由图可得x2>-1,
即-
| 1 |
| a |
∵a>0,
∴a>1;正确.
所以正确的个数是3个.
故选D.
点评:本题主要考查了二次函数图象与系数的关系.解题的关键是根与系数的灵活运用.

练习册系列答案
相关题目
2013年11月9日是国人的骄傲的日子,有约1.2亿中国人关注了广州恒大队与韩国首尔FC队的亚洲冠军杯决赛,最终广州恒大队不负众望夺取冠军,其中1.2亿用科学记数法可表示为( )
| A、12×108 |
| B、1.28 |
| C、0.12×109 |
| D、1.2×108 |
 将1~13这13个数中挑出12个数,填入图中的方格中,使每一横行四个数的和相等,每一数列三个数的和也相等.
将1~13这13个数中挑出12个数,填入图中的方格中,使每一横行四个数的和相等,每一数列三个数的和也相等. 如图,A,B是双曲线y=
如图,A,B是双曲线y=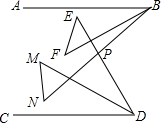 如图,AB∥CD,求∠ABF+∠E+∠F+∠EPN+∠M+∠N+∠CDM的度数是
如图,AB∥CD,求∠ABF+∠E+∠F+∠EPN+∠M+∠N+∠CDM的度数是 如图,正比例函数y=kx与反比例函数y=-
如图,正比例函数y=kx与反比例函数y=-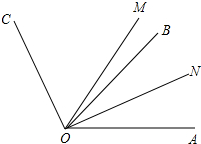 如图,已知ON是∠AOB的平分线,OM、OC是∠AOB外的射线.
如图,已知ON是∠AOB的平分线,OM、OC是∠AOB外的射线.