题目内容
 如图,A,B是双曲线y=
如图,A,B是双曲线y=| k |
| x |
考点:反比例函数的性质,待定系数法求一次函数解析式
专题:证明题
分析:设A(x1,
),B(x2,
),则C(0,
),D(x2,0),然后表示出两条直线的斜率,根据两条直线的斜率相等判定两条直线平行即可.
| k |
| x1 |
| k |
| x2 |
| k |
| x1 |
解答:解:设A(x1,
),B(x2,
),
则C(0,
),D(x2,0),
∴kAB=
=
=-
,
kCD=
=-
,
∴kAB=kCD,
∴AB∥CD.
| k |
| x1 |
| k |
| x2 |
则C(0,
| k |
| x1 |
∴kAB=
| ||||
| x1-x2 |
k•
| ||
| x1-x2 |
| k |
| x1x2 |
kCD=
| ||
| x2 |
| k |
| x1x2 |
∴kAB=kCD,
∴AB∥CD.
点评:本题考查了反比例函数的性质:当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限.

练习册系列答案
相关题目
PM2.5是指大气中直径小于或等于0.0000025米的颗粒物,也称为可入肺颗粒物.它的直径还不到人的头发丝粗细的
.虽然PM2.5只是地球大气成分中含量很少的组分,但它对空气质量和能见度等有重要的影响.与较粗的大气颗粒物相比,PM2.5粒径小,富含大量的有毒、有害物质且在大气中的停留时间长、输送距离远,因而对人体健康和大气环境质量的影响更大,其中0.0000025米用科学记数法表示为( )
| 1 |
| 20 |
| A、25×10-6米 |
| B、2.5×10-6米 |
| C、0.25×10-7米 |
| D、2.5×10-7米 |
一元二次方程2x2+2
x+1=0的根的情况是( )
| 2 |
| A、方程有两个不相等的实数根 |
| B、方程有两个相等的实数根 |
| C、方程没有实数根 |
| D、方程根的情况不能确定 |
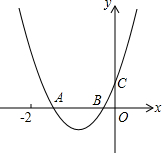 如图,二次函数y=ax2+bx+c的图象与X轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2,②b2-4ac<4a2,③a>1,其中正确的个数为( )
如图,二次函数y=ax2+bx+c的图象与X轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2,②b2-4ac<4a2,③a>1,其中正确的个数为( )| A、0个 | B、1个 | C、2个 | D、3个 |
 如图,DH∥GE,AF平分∠HAB,CB平分∠GCF,若∠F比∠B的两倍少60°,则∠BAH=
如图,DH∥GE,AF平分∠HAB,CB平分∠GCF,若∠F比∠B的两倍少60°,则∠BAH=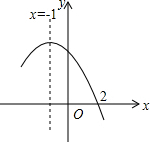 如图所示的是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是x=-1,有下列结论:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),(-4,y2)是抛物线上两点,则y1>y2,其中结论正确的序号是( )
如图所示的是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是x=-1,有下列结论:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),(-4,y2)是抛物线上两点,则y1>y2,其中结论正确的序号是( )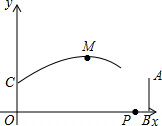 在一次足球赛中,甲运动员在距对方球门AB正前方19.8m的点O处起跳到距地面2m的点C处接队友的传球,用头球攻对方球门,球门AB的高度为2.44m,球的运动轨迹看作抛物线的一部分,当球运动到最高点M时的高度为6m,离甲运动员起跳点O的水平距离为10m,以O为原点建立如图所示的坐标系.
在一次足球赛中,甲运动员在距对方球门AB正前方19.8m的点O处起跳到距地面2m的点C处接队友的传球,用头球攻对方球门,球门AB的高度为2.44m,球的运动轨迹看作抛物线的一部分,当球运动到最高点M时的高度为6m,离甲运动员起跳点O的水平距离为10m,以O为原点建立如图所示的坐标系.