题目内容
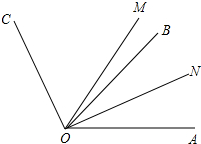 如图,已知ON是∠AOB的平分线,OM、OC是∠AOB外的射线.
如图,已知ON是∠AOB的平分线,OM、OC是∠AOB外的射线.(1)如果∠AOC=α,∠BOC=β,请用含有α,β的式子表示∠NOC.
(2)如果∠BOC=90°,OM平分∠AOC,那么∠MON的度数是多少?
考点:角平分线的定义
专题:
分析:(1)先求出∠AOB=α-β,再利用角平分线求出∠AON,即可得出∠NOC;
(2)先利用角平分线求出∠AOM=
∠AOC,∠AON=
∠AOB,即可得出∠MON=
∠BOC.
(2)先利用角平分线求出∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵∠AOC=α,∠BOC=β,
∴∠AOB=α-β,
∵ON是∠AOB的平分线,
∴∠AON=
(α-β),
∠NOC=α-
(α-β)=
(α+β);
(2)∵OM平分∠AOC,ON平分∠AOB,
∴∠AOM=
∠AOC,∠AON=
∠AOB,
∴∠MON=∠AOM-∠AON=
(∠AOC-∠AOB)=
∠BOC=
×90°=45°.
∴∠AOB=α-β,
∵ON是∠AOB的平分线,
∴∠AON=
| 1 |
| 2 |
∠NOC=α-
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵OM平分∠AOC,ON平分∠AOB,
∴∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠AOM-∠AON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了角平分线的定义和角的计算;弄清各个角之间的数量关系是解决问题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
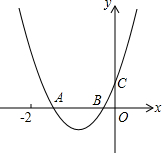 如图,二次函数y=ax2+bx+c的图象与X轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2,②b2-4ac<4a2,③a>1,其中正确的个数为( )
如图,二次函数y=ax2+bx+c的图象与X轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2,②b2-4ac<4a2,③a>1,其中正确的个数为( )| A、0个 | B、1个 | C、2个 | D、3个 |
 如图,已知△ABC中,∠C=90°,AC=BC=2
如图,已知△ABC中,∠C=90°,AC=BC=2| 2 |
A、2-
| ||||
B、
| ||||
C、2(
| ||||
| D、1 |
下列不是平移现象的是( )
| A、站在运行着电梯上的人 |
| B、小刘荡秋千的运动 |
| C、左右推动的窗户 |
| D、躺在火车上睡觉的人 |
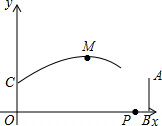 在一次足球赛中,甲运动员在距对方球门AB正前方19.8m的点O处起跳到距地面2m的点C处接队友的传球,用头球攻对方球门,球门AB的高度为2.44m,球的运动轨迹看作抛物线的一部分,当球运动到最高点M时的高度为6m,离甲运动员起跳点O的水平距离为10m,以O为原点建立如图所示的坐标系.
在一次足球赛中,甲运动员在距对方球门AB正前方19.8m的点O处起跳到距地面2m的点C处接队友的传球,用头球攻对方球门,球门AB的高度为2.44m,球的运动轨迹看作抛物线的一部分,当球运动到最高点M时的高度为6m,离甲运动员起跳点O的水平距离为10m,以O为原点建立如图所示的坐标系.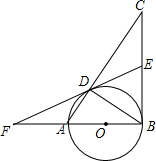 如图,在△ABC中,∠ABC=90°,AB=6,BC=8,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于点F.
如图,在△ABC中,∠ABC=90°,AB=6,BC=8,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于点F. 如图,AB=AC,CE⊥AC,CE⊥AB,垂足分别是D,E,BD,CE相交于点M,点M在∠A的平分线上吗?证明你的结论.
如图,AB=AC,CE⊥AC,CE⊥AB,垂足分别是D,E,BD,CE相交于点M,点M在∠A的平分线上吗?证明你的结论.