题目内容
14.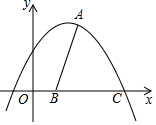 已知抛物线的解析式为y=-$\frac{1}{20}$x2+bx+5.
已知抛物线的解析式为y=-$\frac{1}{20}$x2+bx+5.(1)当自变量x≥2时,函数值y随x的增大而减少,求b的取值范围;
(2)如图,若抛物线的图象经过点A(2,5),与x轴交于点C,抛物线的对称轴与x轴交于B.
①求抛物线的解析式;
②在抛物线上是否存在点P,使得∠PAB=∠ABC?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)由题意可知:对称轴只需要小于或等于2即可,从而可求出b的范围;
(2)①将A代入抛物线解析式即可求出b的值.
②由于∠PAB=∠ABC,且P在抛物线上,故需要对P的位置进行分类讨论即可.
解答 解:(1)抛物线的对称轴为:x=10b,
由题意可知:x≥2时,函数值y 随 x的增大而减少,
∴10b≤2,
∴b≤$\frac{1}{5}$;
(2)①将A(2,5)代入抛物线的解析式中,
∴5=-$\frac{1}{20}$×4+2b+5,
∴b=$\frac{1}{10}$,
∴抛物线的解析式为:y=-$\frac{1}{20}$x2+$\frac{1}{10}$x+5,
②由于∠PAB=∠ABC,
当P在对称轴的左侧时,
此时∠PAB=∠ABC,
∴PA∥BC,
∴P的纵坐标与A的纵坐标相同,
∴P(0,5),
当P在对称轴的右侧时,
连接AP并延长交x轴于E,
此时∠PAB=∠ABC
∴AE=BE,
过点A作AG⊥x轴于点G,过点P作PH⊥x轴于点H,过点E作EF⊥AB于点F,
∵B(1,0),A(2,5),
∴AG=5,BG=1,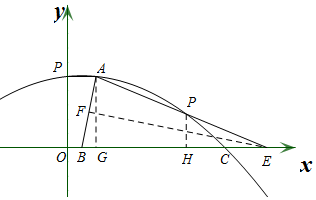
∴由勾股定理可知:AB=$\sqrt{26}$,
∵AE=BE,EF⊥AB,
∴BF=$\frac{1}{2}$AB=$\frac{\sqrt{26}}{2}$,
∵cos∠ABC=$\frac{BG}{AB}$=$\frac{\sqrt{26}}{26}$,
∴cos∠ABC=$\frac{BF}{BE}$=$\frac{\sqrt{26}}{26}$,
∴BE=13,
∴GE=BE-BG=12,
∴tan∠PEG=$\frac{AG}{GE}$=$\frac{5}{12}$,
设P(x,-$\frac{1}{20}$x2+$\frac{1}{10}$x+5),
∵E(14,0),
∴HE=14-x,PH=-$\frac{1}{20}$x2+$\frac{1}{10}$x+5,
∴tan∠PEG=$\frac{PH}{HE}$=$\frac{5}{12}$,
即$\frac{-\frac{1}{20}{x}^{2}+\frac{1}{10}x+5}{14-x}$=$\frac{5}{12}$,
解得:x=2(舍去)或x=$\frac{25}{3}$,
∴P($\frac{25}{3}$,$\frac{85}{36}$)
综上所述,P(0,5)或P($\frac{25}{3}$,$\frac{85}{36}$)
点评 本题考查二次函数的综合问题,涉及勾股定理,二次函数的性质,等腰三角形的性质,锐角三角函数等知识,综合程度较高,需要学生灵活运用所学知识.

 阅读快车系列答案
阅读快车系列答案| A. | 4.4×106 | B. | 44×105 | C. | 4×106 | D. | 0.44×107 |
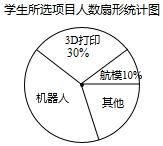 初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.男、女生所选项目人数统计表
| 项目 | 男生(人数) | 女生(人数) |
| 机器人 | 7 | 9 |
| 3D打印 | m | 4 |
| 航模 | 2 | 2 |
| 其他 | 5 | n |
(1)m=8,n=3;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为144°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
| A. | 不在同一直线上的三点确定一个圆 | |
| B. | 角平分线上的点到角两边的距离相等 | |
| C. | 正六边形的内角和是720° | |
| D. | 角的边越大,角就越大 |
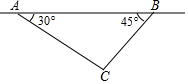 如图所示,飞机在一定高度上沿水平直线飞行,先在点A处测得正前方小岛C的俯角为30°,面向小岛方向继续飞行10km到达B处,发现小岛在其正后方,此时测得小岛的俯角为45°,如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
如图所示,飞机在一定高度上沿水平直线飞行,先在点A处测得正前方小岛C的俯角为30°,面向小岛方向继续飞行10km到达B处,发现小岛在其正后方,此时测得小岛的俯角为45°,如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).