题目内容
4.如图,矩形纸片ABCD中,AB=5,BC=3,先按图(2)操作:将矩形纸片ABCD沿过点A的直线折叠,使点D落在边AB上的点E处,折痕为AF;再按图(3)操作,沿过点F的直线折叠,使点C落在EF上的点H处,折痕为FG,则A、H两点间的距离为$\sqrt{10}$.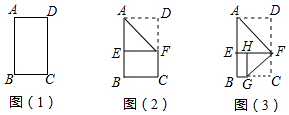
分析 如图3中,连接AH.由题意可知在Rt△AEH中,AE=AD=3,EH=EF-HF=3-2=1,根据AH=$\sqrt{A{E}^{2}+E{H}^{2}}$,计算即可.
解答 解:如图3中,连接AH.
由题意可知在Rt△AEH中,AE=AD=3,EH=EF-HF=3-2=1,
∴AH=$\sqrt{A{E}^{2}+E{H}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
故答案为$\sqrt{10}$.
点评 本题考查翻折变换、矩形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
19.下列运算正确的是( )
| A. | a+2a=3a2 | B. | a3•a2=a5 | C. | (a4)2=a6 | D. | a4+a2=a4 |
9.关于x的一元二次方程x2+(a2-2a)x+a-1=0的两个实数根互为相反数,则a的值为( )
| A. | 2 | B. | 0 | C. | 1 | D. | 2或0 |
2.不能被2整除的数一定是( )
| A. | 奇数 | B. | 素数 | C. | 合数 | D. | 素因数 |
19.下列各题去括号错误的是( )
| A. | x-(3y-0.5)=x-3y+0.5 | B. | m+(-n+a-b)=m-n+a-b | ||
| C. | -0.5(4x-6y+3)=-2x+3y+3 | D. | (a+0.5b)-(-$\frac{1}{3}$c+$\frac{2}{7}$)=a+0.5b+$\frac{1}{3}$c-$\frac{2}{7}$ |
20.如果a>b,那么下列不等式中正确的是( )
| A. | a-b<0 | B. | a+3<b-3 | C. | ac2>bc2 | D. | -$\frac{a}{7}$<-$\frac{b}{7}$ |
 已知抛物线的解析式为y=-$\frac{1}{20}$x2+bx+5.
已知抛物线的解析式为y=-$\frac{1}{20}$x2+bx+5.