题目内容
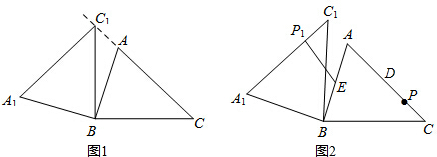
5. 如图所示,△ABC是等边三角形,D是AC的中点,延长BC到E,使CE=$\frac{1}{2}$BC,等于30°的角有4个.
如图所示,△ABC是等边三角形,D是AC的中点,延长BC到E,使CE=$\frac{1}{2}$BC,等于30°的角有4个.
分析 先根据等边三角形的性质得出∠ACB=60°,由CE=CD可知∠E=∠EDC,再根据三角形外角的性质即可得出结论.
解答 解:∵△ABC是等边三角形 (已知),
∴∠ABC=60°(等边三角形性质),
∵D是AC的中点,
∴∠ABD=∠CBD=30°,
∵CE=CD(已知),
∴∠E=∠EDC(等边对等角).
∵∠ACB=∠E+∠EDC(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠E=∠EDC=30°,
故等于30°的角有4个.
故答案为:4.
点评 本题考查了等边三角形和等腰三角形的性质.解题的关键是利用等腰三角形的三线合一的性质.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
10.下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行.
(2)过一点有且只有一条直线与已知直线垂直.
(3)在同一平面内,两条直线的位置关系只有相交、平行两种.
(4)不相交的两条直线叫做平行线.
(5)有公共顶点且有一条公共边的两个角互为邻补角.
(1)过一点有且只有一条直线与已知直线平行.
(2)过一点有且只有一条直线与已知直线垂直.
(3)在同一平面内,两条直线的位置关系只有相交、平行两种.
(4)不相交的两条直线叫做平行线.
(5)有公共顶点且有一条公共边的两个角互为邻补角.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.下列方程一定是一元二次方程的是( )
| A. | (a2+1)x2+bx+c=0 | B. | 5x2-6y-3=0 | C. | ax2-x+2=0 | D. | 3x2+$\frac{2}{x}$-1=0 |
15.使代数式$\frac{\sqrt{2x+1}}{x-1}$有意义的x的取值范围是( )
| A. | x≠1 | B. | x≥-$\frac{1}{2}$且x≠1 | C. | x≥-$\frac{1}{2}$ | D. | x>-$\frac{1}{2}$且x≠1 |