题目内容
在关于x的方程2x2-4x+k=1中,根的判别式的值是8,求k的值,并解这个方程.
考点:根的判别式
专题:
分析:用k表示出根的判别式,令其为8可求得k的值,再解方程即可.
解答:解:
∵2x2-4x+k=1可化为2x2-4x+k-1=0,
∴△=16-8(k-1),
根据题意可得16-8(k-1)=8,解得k=2,
∴原方程为2x2-4x+1=0,
∴x=
=1±
,
即方程的解为x=1+
或x=1-
.
∵2x2-4x+k=1可化为2x2-4x+k-1=0,
∴△=16-8(k-1),
根据题意可得16-8(k-1)=8,解得k=2,
∴原方程为2x2-4x+1=0,
∴x=
4±
| ||
| 4 |
| ||
| 2 |
即方程的解为x=1+
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查根的判别式及一元二次方程的解法,掌握一元二次方程根的判别式为△=b2-4ac是解题的关键.

练习册系列答案
相关题目
 如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙的长为18米,在与墙垂直的一边要开一扇2米宽的门,已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库的宽和长分别为多少米?
如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙的长为18米,在与墙垂直的一边要开一扇2米宽的门,已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库的宽和长分别为多少米? 如图,AD是△ABC中BC边上的中线,若AB=5,AC=4,则AD不可能是( )
如图,AD是△ABC中BC边上的中线,若AB=5,AC=4,则AD不可能是( )| A、2 | B、3 | C、4 | D、5 |
若已知a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,则a、b、c三个数的和是( )
| A、1 | B、0 | C、-1 | D、不存在 |
长城总长约为6 700 000米,用科学记数法表示正确的是( )
| A、6.7×108米 |
| B、6.7×107米 |
| C、6.7×106米 |
| D、6.7×105米 |
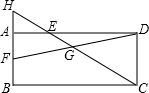 如图,在矩形ABCD中,E、F分别是AD、AB边上的点,连接CE、DF,他们相交于点G,延长CE交BA的延长线于点H,则图中的相似三角形共有( )
如图,在矩形ABCD中,E、F分别是AD、AB边上的点,连接CE、DF,他们相交于点G,延长CE交BA的延长线于点H,则图中的相似三角形共有( )