题目内容
18.已知A=5x2-mx+n,B=3y2-2x-1(A、B为关于x,y的多项式),如果A-B的结果中不含一次项和常数项.(1)求:m、n的值;
(2)求:m2+n2-2mn的值.
分析 (1)把A与B代入A-B中,去括号合并后由结果不含一次项与常数项求出m与n的值即可;
(2)把m与n的值代入原式计算即可得到结果.
解答 解:(1)∵A=5x2-mx+n,B=3y2-2x-1,
∴A-B=5x2-mx+n-3y2+2x+1=5x2-3y2+(2-m)x+n+1,
由结果中不含一次项和常数项,得到2-m=0,n+1=0,
解得:m=2,n=-1;
(2)当m=2,n=-1时,原式=4+1+4=9.
点评 此题考查了整式的加减,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图中字母A所代表的正方形的面积为( )
如图中字母A所代表的正方形的面积为( )
 如图中字母A所代表的正方形的面积为( )
如图中字母A所代表的正方形的面积为( )| A. | 12 | B. | 5 | C. | 10 | D. | 25 |
6.已知-3xm-1y3与$\frac{5}{2}$xym+n是同类项,那么m,n的值分别是( )
| A. | m=2,n=-1 | B. | m=-2,n=-1 | C. | m=-2,n=1 | D. | m=2,n=1 |
3. 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )| A. | 甲乙两人8分钟各跑了800米 | |
| B. | 前2分钟,乙的平均速度比甲快 | |
| C. | 5分钟时两人都跑了500米 | |
| D. | 甲跑完800米的平均速度为100米∕分 |
10.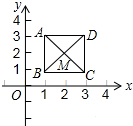 如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
 如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )| A. | (-2012,2) | B. | (-2012,-2) | C. | (-2013,-2) | D. | (-2013,2) |
8.下列说法正确的是( )
| A. | 带有“+”号的数是正数 | |
| B. | 带有“-”号的数是负数 | |
| C. | 数轴上的两个点可以表示同一个有理数 | |
| D. | 有理数分为自然数、负整数、分数 |
 已知:抛物线y=ax2-2(a-1)x+a-2(a>0).
已知:抛物线y=ax2-2(a-1)x+a-2(a>0).