题目内容
5.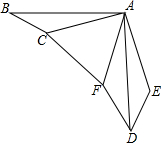 如图,在△ABC中,∠BAC=15°,将△ABC绕点A按逆时针方向旋转90°,到△ADE的位置,然后将△ADE以AD为轴翻折到△ADF的位置,连接CF,判断△ACF的形状,并说明理由.
如图,在△ABC中,∠BAC=15°,将△ABC绕点A按逆时针方向旋转90°,到△ADE的位置,然后将△ADE以AD为轴翻折到△ADF的位置,连接CF,判断△ACF的形状,并说明理由.
分析 由旋转和翻折的性质可知:AC=AF,然后再求得∠CAF=60°,从而可得出△ACF为等边三角形.
解答 解:由旋转的性质可知:∠BAC=∠DAE=15°,AC=AE,∠CAE=90°,
由翻折的性质可知:∠FAD=∠EAD=15°,AF=AE.
∴AC=AF,∠CAF=60°,
∴△ACF为等边三角形.
点评 本题主要考查的是翻折变换、旋转变换、等边三角形的性质和判定,证得AC=AF,∠CAF=60°是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
16.对于抛物线y=5x2+l,有下列说法:
①抛物线与y轴的交点坐标为(1,0);
②抛物线和x轴交于两点;
③将其向右平移2个单位.再向上平移3个单位.得到的抛物线是y=5(x+2)2+4;
④当x>0时,y随x的增大而增大.
其中正确的个数为( )
①抛物线与y轴的交点坐标为(1,0);
②抛物线和x轴交于两点;
③将其向右平移2个单位.再向上平移3个单位.得到的抛物线是y=5(x+2)2+4;
④当x>0时,y随x的增大而增大.
其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.如果点A的坐标满足xy=0,则点A必在( )
| A. | x轴上 | B. | y轴上 | C. | 原点 | D. | 坐标轴上 |
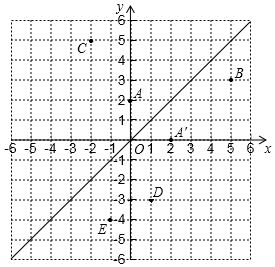 如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.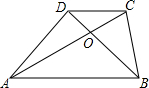 已知,如图,四边形ABCD的对角线AC,BD交于点O,S△AOD=S△BOC,求证:$\frac{DO}{OB}$=$\frac{CO}{OA}$.
已知,如图,四边形ABCD的对角线AC,BD交于点O,S△AOD=S△BOC,求证:$\frac{DO}{OB}$=$\frac{CO}{OA}$.