题目内容
 (1)已知反比例函数y=
(1)已知反比例函数y=| k |
| x |
(2)如图,为了测量池塘的宽BC,学校测量组在直线BC上的A点测得AB为4米,且∠DAC=90°,在D点测得AD=12米,且∠ADC=65°,求池塘的宽BC(结果精确到0.1米)(参考数据sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
考点:解直角三角形的应用,反比例函数图象上点的坐标特征
专题:
分析:(1)直接把点(1,-2)代入反比例函数y=
求出k的值,进而可得出反比例函数的解析式,把x=-6代入求出y的值即可;
(2)在Rt△ADC中根据锐角三角函数的定义求出AC的长,根据BC=AC-AB即可得出结论.
| k |
| x |
(2)在Rt△ADC中根据锐角三角函数的定义求出AC的长,根据BC=AC-AB即可得出结论.
解答:解:(1)∵反比例函数y=
的图象经过点(1,-2),
∴-2=
,解得k=-2,
∴反比例函数的解析式为y=-
,
当x=-6时,y=-
=
;
(2)∵在Rt△ADC中,AD=12米,且∠ADC=65°,
∴AC=AD•tan∠ADC
=12×2.14
=25.68(米),
∴BC=AC-AB=25.68-4=21.68≈21.7(米).
答:池塘的宽BC为21.7米.
| k |
| x |
∴-2=
| k |
| 1 |
∴反比例函数的解析式为y=-
| 2 |
| x |
当x=-6时,y=-
| 2 |
| -6 |
| 1 |
| 3 |
(2)∵在Rt△ADC中,AD=12米,且∠ADC=65°,
∴AC=AD•tan∠ADC
=12×2.14
=25.68(米),
∴BC=AC-AB=25.68-4=21.68≈21.7(米).
答:池塘的宽BC为21.7米.
点评:本题考查的是解直角三角形的应用,熟知锐角三角函数的定义是解答此题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,AB=AC,∠ABC=70°,∠ABC的角平分线及△ABC的外角平分线相交于D,则∠CAD的度数是
如图,AB=AC,∠ABC=70°,∠ABC的角平分线及△ABC的外角平分线相交于D,则∠CAD的度数是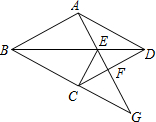 如图,四边形ABCD为菱形,点G为BC的延长线上一点,连接AG,分别交BD、DC于点E、F,连CE.
如图,四边形ABCD为菱形,点G为BC的延长线上一点,连接AG,分别交BD、DC于点E、F,连CE.
 如图,AB为⊙O的直径,以AB为直角边作Rt△ABC,∠CAB=90°,斜边BC与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥AB于点F,交⊙O于点G.
如图,AB为⊙O的直径,以AB为直角边作Rt△ABC,∠CAB=90°,斜边BC与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥AB于点F,交⊙O于点G. 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为