题目内容
3.解方程组:$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-xy-3x+3=0}\\{{x}^{2}+{y}^{2}+{z}^{2}-xy-yz-2xz-9=0}\end{array}\right.$.分析 把①化为($\frac{1}{2}$x-y)2+$\frac{3}{4}$(x-2)2=0的形式,从中求出x、y的值,把x、y的值代入方程②求出z的值,得到方程组的解.
解答 解:$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-xy-3x+3=0①}\\{{x}^{2}+{y}^{2}+{z}^{2}-xy-yz-2xz-9=0②}\end{array}\right.$
有①得,
($\frac{1}{2}$x-y)2+$\frac{3}{4}$(x-2)2=0
解得,x=2,y=1,
把x=2,y=1代入②得,
z2-5z-6=0
z1=-1,z2=6
所以方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=-1}\end{array}\right.$,$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=6}\end{array}\right.$
点评 本题考查的是三元二次方程组的解法,解题的关键是通过配方法找出x、y的关系,然后代入求值.

练习册系列答案
相关题目
10.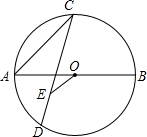 如图,AB是⊙O的直径,点C是半圆的中点,连接AC,CD是弦.若AB=10,tan∠ACD=$\frac{3}{4}$,CA=CE,连接OE,则OE的长为( )
如图,AB是⊙O的直径,点C是半圆的中点,连接AC,CD是弦.若AB=10,tan∠ACD=$\frac{3}{4}$,CA=CE,连接OE,则OE的长为( )
 如图,AB是⊙O的直径,点C是半圆的中点,连接AC,CD是弦.若AB=10,tan∠ACD=$\frac{3}{4}$,CA=CE,连接OE,则OE的长为( )
如图,AB是⊙O的直径,点C是半圆的中点,连接AC,CD是弦.若AB=10,tan∠ACD=$\frac{3}{4}$,CA=CE,连接OE,则OE的长为( )| A. | $\sqrt{5}$ | B. | $\frac{5}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{5}{3}$ |
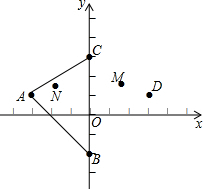 在图中,三角形DBC是由三角形ABC经过某种变换后得到的图形,分别写出点A、B、C、D的坐标.观察点A与点D的坐标之间的关系,如果三角形ABC中任一点N的坐标为N(x,y),它的对应点M的坐标是什么?
在图中,三角形DBC是由三角形ABC经过某种变换后得到的图形,分别写出点A、B、C、D的坐标.观察点A与点D的坐标之间的关系,如果三角形ABC中任一点N的坐标为N(x,y),它的对应点M的坐标是什么?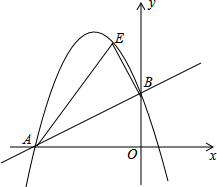 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=-x2+bx+c,点E为第二象限内抛物线上一动点,连接AE,BE.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=-x2+bx+c,点E为第二象限内抛物线上一动点,连接AE,BE. 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标为($\frac{3}{2}$,3).
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标为($\frac{3}{2}$,3).