题目内容
4.关于x的一元二次方程x2+2(m+1)x+(3m2+4mn+4n2+2)=0有实数根,则3m2+2n3=$\frac{11}{4}$.分析 根据方程有实数根结合根的判别式即可得出-4(m-1)2-4(m+2n)2≥0,由偶次方非负即可得出关于m、n的二元一次方程,解方程组即可得出m、n的值,将其代入3m2+2n3中即可得出结论.
解答 解:∵方程x2+2(m+1)x+(3m2+4mn+4n2+2)=0有实数根,
∴△=[2(m+1)]2-4×1×(3m2+4mn+4n2+2)=-4(m-1)2-4(m+2n)2≥0,
∴$\left\{\begin{array}{l}{m-1=0}\\{m+2n=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=1}\\{n=-\frac{1}{2}}\end{array}\right.$,
∴3m2+2n3=3×12+2×$(-\frac{1}{2})^{3}$=$\frac{11}{4}$.
故答案为:$\frac{11}{4}$.
点评 本题考查了根的判别式以及解二元一次方程组,根据偶次方非负得出关于m、n的二元一次方程组是解题的关键.

练习册系列答案
相关题目
 如图,将长、宽分别为40cm,20cm的长方形玻璃裁成两部分,然后拼成一个直角三角形,画出图形,并注明各边的长度.
如图,将长、宽分别为40cm,20cm的长方形玻璃裁成两部分,然后拼成一个直角三角形,画出图形,并注明各边的长度.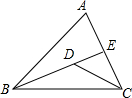 如图在△ABC中,D是∠ACB与∠ABC的角平分线的交点,BD的延长线交AC于E,且∠EDC=50°,则∠A的度数为80°.
如图在△ABC中,D是∠ACB与∠ABC的角平分线的交点,BD的延长线交AC于E,且∠EDC=50°,则∠A的度数为80°.