题目内容
10.在平行四边形ABCD中,AE垂直于对角线BD,垂足为E,连接CE.若三角形BCE是等边三角形,CD=2$\sqrt{7}$,则BD=6.分析 利用等边三角形的性质得,∠CBE=60°,BC=BE,再根据平行四边形的性质得AB=CD=2$\sqrt{7}$,BC=AD,AD∥BC,则∠ADE=60°,接着在Rt△ADE中,设DE=x,利用含30度的直角三角形三边的关系得到AE=$\sqrt{3}$x,AD=2x,则BC=BE=2x,然后根据勾股定理得到($\sqrt{3}$x)2+(2x)2=(2$\sqrt{7}$)2,解得x=2,最后计算DE+BE即可.
解答 解:∵△BCE为等边三角形,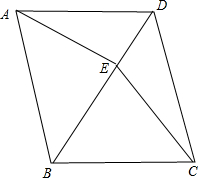
∴∠CBE=60°,BC=BE,
∵四边形ABCD为平行四边形,
∴AB=CD=2$\sqrt{7}$,BC=AD,AD∥BC,
∴∠ADE=60°,
∵AE⊥BD,
在Rt△ADE中,设DE=x,则AE=$\sqrt{3}$x,AD=2x,
∴BC=BE=2x,
在Rt△ABE中,∵AE2+BE2=AB2,
∴($\sqrt{3}$x)2+(2x)2=(2$\sqrt{7}$)2,解得x=2,
∴BD=x+2x=3x=6.
故答案为6.
点评 本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.也考查了等边三角形的性质.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
18.一个扇形的弧长是10πcm,面积是60πcm2,则此扇形的圆心角的度数是( )
| A. | 300° | B. | 150° | C. | 120° | D. | 75° |
15.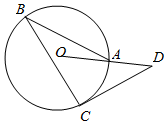 如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
 如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )| A. | 29° | B. | 32° | C. | 42° | D. | 58° |
2.计算:(-$\frac{1}{2}$)2-1=( )
| A. | -$\frac{5}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | 0 |
19.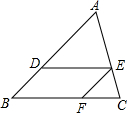 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
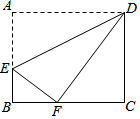 如图,矩形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE,若AB=8,BF=4,则BC=10cm.
如图,矩形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE,若AB=8,BF=4,则BC=10cm.

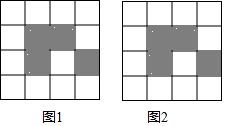 如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.