题目内容
20.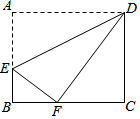 如图,矩形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE,若AB=8,BF=4,则BC=10cm.
如图,矩形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE,若AB=8,BF=4,则BC=10cm.
分析 设AE=x,表示出BE,根据翻折变换的性质可得EF=AE,然后利用勾股定理列出方程求解即可得到EF的长,再根据相似三角形的性质,即可得到CF的长,进而得出BC的长.
解答 解:设EF=AE=x,则BE=8-x,
∵∠B=90°,BF=4,
∴Rt△BEF中,BE2+BF2=EF2,
即(8-x)2+42=x2,
解得x=5,
∴EF=5,BE=3,
∵∠DFE=∠A=90°,∠C=90°,
∴∠CDF=∠BFE,
又∵∠B=∠C=90°,
∴△DCF∽△FBE,
∴$\frac{CF}{BE}$=$\frac{CD}{BF}$,即$\frac{CF}{3}$=$\frac{8}{4}$,
∴CF=6,
∴BC=BF+CF=4+6=10.
故答案为:10.
点评 本题考查了翻折变换的性质,勾股定理以及相似三角形的性质的运用,熟记折叠的性质并利用勾股定理列出方程是解题的关键.解题时注意方程思想的运用.

练习册系列答案
相关题目
9.从一副洗匀的普通扑克牌中随机抽取一张,则抽出红桃的概率是( )
| A. | $\frac{1}{54}$ | B. | $\frac{13}{54}$ | C. | $\frac{1}{13}$ | D. | $\frac{1}{4}$ |
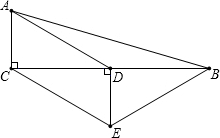 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,垂足为点D,CE∥AD,若AC=2,CE=4.
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,垂足为点D,CE∥AD,若AC=2,CE=4. 在Rt△ABC中,∠C=90°,∠A=30°,AB=6,点D,E分别是BC,AB上的动点,将△BDE沿直线DE翻折,点B的对应点B′恰好落在AC上,若△AEB′是等腰三角形,那么CB′的值是3,3$\sqrt{2}$-3,0.
在Rt△ABC中,∠C=90°,∠A=30°,AB=6,点D,E分别是BC,AB上的动点,将△BDE沿直线DE翻折,点B的对应点B′恰好落在AC上,若△AEB′是等腰三角形,那么CB′的值是3,3$\sqrt{2}$-3,0. 如图,已知BD是△ABC的角平分线,DE∥AB交BC于E,EF∥AC交AB于F.
如图,已知BD是△ABC的角平分线,DE∥AB交BC于E,EF∥AC交AB于F.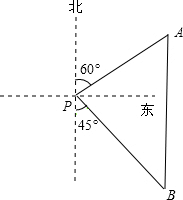 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为102n mile.(结果取整数,参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为102n mile.(结果取整数,参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)