Question

10．已知圆的半径为5，弦AB∥CD，且AB=8，CD=6，则弦AB与CD的距离为1或7．

Answer 1

分析 分两种情况考虑：当两条弦位于圆心O一侧时，如图1所示，过O作OE⊥CD，交CD于点E，交AB于点F，连接OA，OC，由AB∥CD，得到OE⊥AB，利用垂径定理得到E与F分别为CD与AB的中点，在直角三角形AOF中，利用勾股定理求出OF的长，在三角形COE中，利用勾股定理求出OE的长，由OE-OF即可求出EF的长；当两条弦位于圆心O两侧时，如图2所示，同理由OE+OF求出EF的长即可．

解答 解：分两种情况考虑：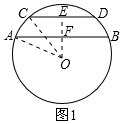
当两条弦位于圆心O一侧时，如图1所示，
过O作OE⊥CD，交CD于点E，交AB于点F，连接OA，OC，
∵AB∥CD，∴OE⊥AB，
∴E、F分别为CD、AB的中点，
∴CE=DE=$\frac{1}{2}$CD=3，AF=BF=$\frac{1}{2}$AB=4，
在Rt△AOF中，OA=5，AF=4，
根据勾股定理得：OF=$\sqrt{O{A}^{2}-A{F}^{2}}$=3，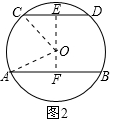
在Rt△COE中，OC=5，CE=3，
根据勾股定理得：OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=4，
则EF=OE-OF=4-3=1；
当两条弦位于圆心O两侧时，如图2所示，
同理可得EF=4+3=7，
综上，弦AB与CD的距离为1或7．
故答案为：1或7．

点评 此题考查了垂径定理，勾股定理，利用了分类讨论的思想，熟练掌握垂径定理是解本题的关键．