题目内容
2. 以下两个问题,任选其一作答.
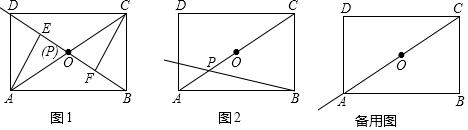
以下两个问题,任选其一作答.如图,OD是∠AOC的平分线,OE是∠BOC的平分线.
问题一:若∠AOC=36°,∠BOC=136°,求∠DOE的度数.
问题二:若∠AOB=100°,求∠DOE的度数.
分析 (1)利用角平分线的定义得出∠DOC=18°,∠EOC=68°进而求出∠DOE的度数;
(2)由角平分线得出∠DOE=$\frac{1}{2}∠AOB$即可.
解答 解:问题一:
∵OD平分∠AOC,∠AOC=36°,
∴$∠DOC=\frac{1}{2}∠AOC=18°$.
∵OE平分∠BOC,∠BOC=136°,
∴$∠EOC=\frac{1}{2}∠BOC=68°$.
∴∠DOE=∠EOC-∠DOC=50°.
问题二:
∵OD平分∠AOC,
∴$∠DOC=\frac{1}{2}∠AOC$.
∵OE平分∠BOC,
∴$∠EOC=\frac{1}{2}∠BOC$.
∴∠DOE=∠EOC-∠DOC=$\frac{1}{2}∠BOC-\frac{1}{2}∠AOC$=$\frac{1}{2}∠AOB$.
∵∠AOB=100°,
∴∠DOE=50°.
点评 此题主要考查了角平分线的定义,得出∠DOE=$\frac{1}{2}$∠AOB是解题关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
11.某项工程甲单独做4天完成,乙单独做6天完成,若甲先做1天,然后甲、乙合作完成此项工程,若设甲一共做了x天,则所列方程为( )
| A. | $\frac{x}{4}$+$\frac{x+1}{6}$=1 | B. | $\frac{x}{4}$+$\frac{x-1}{6}$=1 | C. | $\frac{x+1}{4}$+$\frac{x}{6}$=1 | D. | $\frac{x}{4}$+$\frac{1}{4}$+$\frac{x-1}{6}$=1 |
 如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.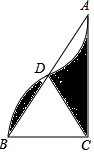 如图,在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点C为圆心,CB的长为半 径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为$\sqrt{3}$.
如图,在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点C为圆心,CB的长为半 径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为$\sqrt{3}$.