题目内容
11.正方形ABCD中,对角线BD长为16cm,P是AB上任意一点,则点P到AC,BD的距离之和等于8cm.分析 作PE⊥OA于E,PF⊥OB于F,由正方形的性质得出OA=OC=OB=OD=$\frac{1}{2}$BD=8cm,OA⊥OB,由S△OPA+S△OPB=S△OAB,得出PE+PF=OA,即可得出结果.
解答 解:作PE⊥OA于E,PF⊥OB于F,连结OP,如图所示,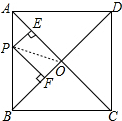
∵四边形ABCD为正方形,
∴OA=OC=OB=OD=$\frac{1}{2}$BD=8cm,OA⊥OB,
∵S△OPA+S△OPB=S△OAB,
∴$\frac{1}{2}$PE•OA+$\frac{1}{2}$PF•OB=$\frac{1}{2}$OA•OB,
∴PE+PF=OA=8cm.
故答案为:8.
点评 本题考查了正方形的性质、三角形面积的计算方法;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
19.若y=(a2+a)${x}^{{a}^{2}-2a-1}$是二次函数,那么( )
| A. | a=-1或a=3 | B. | a≠-1或a≠0 | C. | a=3 | D. | a=-1 |