题目内容
6.$\frac{2{x}^{2}+x}{(x+1)^{3}}$=$\frac{A}{x+1}$+$\frac{B}{(x+1)^{2}}$+$\frac{C}{(x+1)^{3}}$,求A+B+C的值.分析 先把等式的右边通分,再展开,合并同类项,即可得出答案.
解答 解:∵$\frac{2{x}^{2}+x}{(x+1)^{3}}$=$\frac{A}{x+1}$+$\frac{B}{(x+1)^{2}}$+$\frac{C}{(x+1)^{3}}$,
∴$\frac{2{x}^{2}+x}{(x+1)^{3}}$=$\frac{A(x+1)^{2}+B(x+1)+C}{(x+1)^{3}}$,
∴$\frac{2{x}^{2}+x}{(x+1)^{3}}$=$\frac{A{x}^{2}+(2A+B)x+(A+B+C)}{(x+1)^{3}}$,
∴A+B+C=0.
点评 本题考查了分式的加减的应用,能根据分式的运算法则正确进行化简是解此题的关键.

练习册系列答案
相关题目
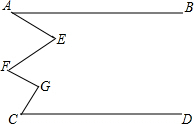 如图,已知直线AB∥CD,试确定∠A,∠F,∠C与∠E,∠G之间的数量关系并说明理由.
如图,已知直线AB∥CD,试确定∠A,∠F,∠C与∠E,∠G之间的数量关系并说明理由.