题目内容
16.如果最简根式-$\sqrt{a+5}$与$\root{2a-b}{9-b}$能够进行合并,则a-b=1.分析 根据同类二次根式的根指数、被开方数相同,可得关于a、b的方程组,解出即可.
解答 解:因为最简根式-$\sqrt{a+5}$与$\root{2a-b}{9-b}$能够进行合并,
可得:$\left\{\begin{array}{l}{2a-b=2}\\{a+5=9-b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$,
所以a-b=2-1=1,
故答案为:1.
点评 本题考查了同类二次根式的知识,解答本题注意掌握同类二次根式的根指数、被开方数相同.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.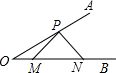 如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )
如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )
 如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )
如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )| A. | 8 | B. | 6 | C. | 2$\sqrt{3}$+4 | D. | 2$\sqrt{3}$+2 |
7.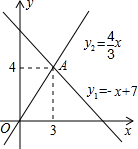 如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
 如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )| A. | x>3 | B. | x<3 | C. | x>4 | D. | x<4 |
 如图,在一块长AB=a cm,宽BC=b cm的长方形草地上,有三条宽都是2m的小路,则这块草地的绿地面积为(a-4)(b-2)cm2.
如图,在一块长AB=a cm,宽BC=b cm的长方形草地上,有三条宽都是2m的小路,则这块草地的绿地面积为(a-4)(b-2)cm2. 如图,在平面直角坐标系中,已知点A(-3,4),B(-1,-2),O为原点,求△AOB的面积.
如图,在平面直角坐标系中,已知点A(-3,4),B(-1,-2),O为原点,求△AOB的面积.