题目内容
6.计算:$\sqrt{3}$($\sqrt{6}$-1)+3$\sqrt{\frac{1}{3}}$+($\sqrt{2}$-1)2.分析 首先利用二次根式混合运算法则去括号整理,进而合并同类二次根式得出答案.
解答 解:原式=3$\sqrt{2}$-$\sqrt{3}$+3×$\frac{\sqrt{3}}{3}$+2-2$\sqrt{2}$+1
=3$\sqrt{2}$-$\sqrt{3}$+$\sqrt{3}$+3-2$\sqrt{2}$
=$\sqrt{2}$+3.
点评 此题主要考查了二次根式的混合运算法则,正确化简二次根式是解题关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
16.?ABCD中,周长等于24,其中一组对边长是8,那么,另一组对边长为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
18.下列计算结果正确的是( )
| A. | 2+$\sqrt{3}$=2$\sqrt{3}$ | B. | $\sqrt{8}÷\sqrt{2}$=2 | C. | (-2a2)3=-6a6 | D. | (a+1)2=a2+1 |
15.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球试验,将球搅匀后,从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近于多少?
(2)假如你去摸一次,你摸到白球的可能性为多大?这时摸到黑球的可能性为多大?
(3)试估算口袋中黑、白两种颜色的球各有多少个?
(1)请估计:当n很大时,摸到白球的频率将会接近于多少?
| 摸球的次数m | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数n | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的概率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(3)试估算口袋中黑、白两种颜色的球各有多少个?
17.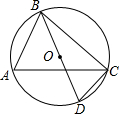 如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )
如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )
 如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )
如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )| A. | $\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |