题目内容
1.观察下列各式:$\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$;$\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$;$\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$,…,请你猜想:
(1)$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$,$\sqrt{5+\frac{1}{7}}$=6$\sqrt{\frac{1}{7}}$;
(2)计算(请写出推导过程):$\sqrt{15+\frac{1}{17}}$=16$\sqrt{\frac{1}{17}}$;
(3)请你将猜想到的规律用含有自然数n(n≥1)的代数式表达出来:$\sqrt{n+\frac{1}{n+2}}=(n+1)\sqrt{\frac{1}{n+2}}$.
分析 (1)观察各式,即可求得答案;
(2)根据所给例子,即可解答;
(3)根据所给例子,即可得到规律.
解答 解:(1)$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$,$\sqrt{5+\frac{1}{7}}$=6$\sqrt{\frac{1}{7}}$.故答案为:5$\sqrt{\frac{1}{6}}$,6$\sqrt{\frac{1}{7}}$;
(2)$\sqrt{15+\frac{1}{17}}$=$\sqrt{\frac{15×17+1}{17}}=\sqrt{\frac{(16-1)×(16+1)-1}{17}}$=$\sqrt{\frac{1{6}^{2}-1+1}{17}}$=$\sqrt{\frac{1{6}^{2}}{17}}=16\sqrt{\frac{1}{17}}$,故答案为:16$\sqrt{\frac{1}{17}}$;
(3)$\sqrt{n+\frac{1}{n+2}}$=$\sqrt{\frac{n(n+2)+1}{n+2}}$=$\sqrt{\frac{(n+1)^{2}}{n+2}}=(n+1)\sqrt{\frac{1}{n+2}}$,
故答案为:$\sqrt{n+\frac{1}{n+2}}=(n+1)\sqrt{\frac{1}{n+2}}$.
点评 此题考查了二次根式的化简问题.此题难度适中,属于规律性题目,注意掌握二次根式的化简知识是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.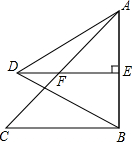 如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.
如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.
(1)求证:△AEF是等腰直角三角形;
(2)求DF的长.
 如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.
如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.(1)求证:△AEF是等腰直角三角形;
(2)求DF的长.
10.判定△ABC∽△A′B′C′,已知∠C′=∠C=90°,则应有哪个条件( )
| A. | ∠B=∠B′ | B. | $\frac{A′B′}{AB}$=$\frac{A′C′}{AC}$ | C. | $\frac{B′C′}{BC}$=$\frac{A′C′}{AC}$ | D. | 以上说法都对 |
 如图,AB为⊙0的直径,C为OA的中点,F为OB的中点,CD⊥AB交⊙0于D、EF⊥AB交⊙O于E.
如图,AB为⊙0的直径,C为OA的中点,F为OB的中点,CD⊥AB交⊙0于D、EF⊥AB交⊙O于E.