题目内容
17．
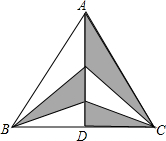如图，△ABC中，AD是BC的中垂线，若BC=8，AD=6，则图中阴影部分的面积是12．
分析 先根据垂直平分线的性质得出AB=AC，BE=CE，BF=CF，根据同底等高的三角形面积相等即可得出S△BEF=S△CEF，由此可得出结论．
解答 
解：∵AD是BC的中垂线，
∵AB=AC，BE=CE，BF=CF．
∵同底等高的三角形面积相等，
∴S△BEF=S△CEF，
∴S阴影=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×8×6=12．
故答案为：12．
点评 本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
练习册系列答案
相关题目
7．如果a，b表示两个实数，那么下列命题正确的是（ ）
| A． | 若a2=b2，则a=b | B． | 若a＜b，则$\sqrt{{a}^{2}}＜\sqrt{{b}^{2}}$ | C． | 若$\root{3}{a}$=$\root{3}{b}$，则$\sqrt{a}=\sqrt{b}$ | D． | 若a＞b，则$\root{3}{a}$$＞\root{3}{b}$ |
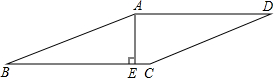如图，在菱形ABCD中，已知AE⊥BC于点E，EC=1，且AE：BE=5：2，求四边形ABCD的周长．
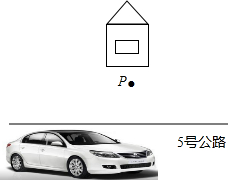如图所示，一次缉毒行动中，警方获可靠信息，一运毒车将经过5号公路，但由于车上有爆炸装置，警方无法靠近，只能使用远程射击的方法，为了减少对周围的伤亡，警方选中一距离公路120m的隐蔽处P点，射程为200m，准备行动，此时发现，运毒车已经来到与P点的水平距离为300m处，若运毒车的车速为20m/s，那警察发现后要在几秒钟内对其进行射击？