题目内容
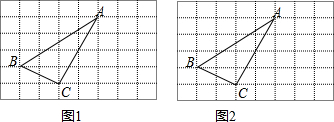
6.在△ABC中,AB=2$\sqrt{3}$,BC=2,∠ABC=60°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为2或2$\sqrt{7}$.分析 利用A,D点在BC的两侧以及A,D点在BC的同侧进而分别利用勾股定理求出答案.
解答 
 解:如图1所示:过点D作DE⊥BC于点E,
解:如图1所示:过点D作DE⊥BC于点E,
∵AB=2$\sqrt{3}$,BC=2,∠ABC=60°,以AB为一边作等腰直角三角形ABD,∠ABD=90°,
∴∠EBD=30°,AB=BD=2$\sqrt{3}$,
则DE=$\frac{1}{2}$BD=$\sqrt{3}$,BE=3,
故EC=1,
则在Rt△DEC中,DC=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
如图2所示:过点D作DE⊥BC于点E,
∵AB=2$\sqrt{3}$,BC=2,∠ABC=60°,以AB为一边作等腰直角三角形ABD,∠ABD=90°,
∴∠EBD=30°,AB=BD=2$\sqrt{3}$,
则DE=$\frac{1}{2}$BD=$\sqrt{3}$,BE=3,
故EC=5,
则在Rt△DEC中,DC=$\sqrt{{5}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{7}$.
故线段CD的长为:2或2$\sqrt{7}$.
点评 此题主要考查了勾股定理以及直角三角形的性质,根据题意结合分类讨论求出是解题关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
14.把拋物线y=(x-1)2+2向右平移1个单位,再向下平移3个单位,所得抛物线是( )
| A. | y=x2+5 | B. | y=(x-2)2-l | C. | y=(x-2)2-3 | D. | y=x2-1 |
11.张先生先到银行存了一笔三年的定期存款,年利率是4.25%,如果到期后取出的本息和为43825元,设张先生存入的本金为x元,则下面所列方程正确的是( )
| A. | x+3×4.25%x=43825 | B. | x+4.25%x=43825 | ||
| C. | 3×4.25%x=43825 | D. | 3(x+4.25%x)=43825 |
 如图,在数轴上有两点A、B,A表示的数为6,B在A的左侧,且AB=10.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动.
如图,在数轴上有两点A、B,A表示的数为6,B在A的左侧,且AB=10.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动. 如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.
如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.