题目内容
16. 如图,在数轴上有两点A、B,A表示的数为6,B在A的左侧,且AB=10.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动.
如图,在数轴上有两点A、B,A表示的数为6,B在A的左侧,且AB=10.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动.(1)请直接写出点B表示的数为-4;
(2)经过多少时间,线段AP和BP的长度之和为18?
(3)若点M、N分别在线段AP和BP上,且AM=2014PM,BN=2014PN.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请画出图形,并求出线段MN的长.
分析 (1)B点表示的数为6-10=-4;
(2)分析题意可知点P在点B的左侧,用t表示出AP和BP的长度,列出一元一次方程,求出t的值;
(3)分类讨论:①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差易求出MN.
解答 解:(1)AB=6-(-4)=10,即点B的数为-4;
(2)若此时P在线段AB上,则AP+BP恒为10,故此时P必在点B的左侧.
设经过t秒,则4t+4t-10=18,
解得t=3.5,
(3)线段MN的长度不发生变化,都等于$\frac{2}{403}$.理由如下:
分两种情况:①当点P在点A、B两点之间运动时:
MN=MP+NP=$\frac{1}{2015}AP+\frac{1}{2015}BP=\frac{1}{2015}(AP+BP)=\frac{1}{2015}AB=\frac{2}{403}$,
②当点P运动到点B的左侧时: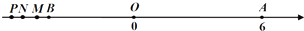
MN=MP-NP=$\frac{1}{2015}AP-\frac{1}{2015}BP=\frac{1}{2015}(AP-BP)=\frac{1}{2015}AB=\frac{2}{403}$,
综上所述,线段MN的长度不发生变化,都等于$\frac{2}{403}$.
点评 本题主要考查了一元一次方程的应用以及数轴和两点间的距离等知识,解答本题的关键是掌握两点间的距离公式,解答第三问注意分类讨论思想,此题难度不大.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
4.2014年12月24日,宁波地铁3号线一期工程正式动工开建,预计总投资148.7亿元,其中148.7亿元用科学记数法表示为( )
| A. | 14.87×109元 | B. | 1.487×109元 | C. | 1.487×1010元 | D. | 0.1487×1011元 |
5.点A(x1,-6)和点B(x2,-3)都在直线y=-3x-5上,则x1和x2的大小关系是( )
| A. | x1=x2 | B. | x1<x2 | C. | x1>x2 | D. | 不能确定 |

 在△ABC中,∠C=90°,AC=3,BC=4,若将△ABC绕点B逆时针旋转90°后,点A的对应点为D,则AD的长为5$\sqrt{2}$.
在△ABC中,∠C=90°,AC=3,BC=4,若将△ABC绕点B逆时针旋转90°后,点A的对应点为D,则AD的长为5$\sqrt{2}$. 已知直线AB的解析式为:y=$\frac{4}{3}$x+4交x轴于点A,交y轴于点B.动点C从A点出发,以每秒2个单位的速度沿x轴正方向运动,设运动时间为t.
已知直线AB的解析式为:y=$\frac{4}{3}$x+4交x轴于点A,交y轴于点B.动点C从A点出发,以每秒2个单位的速度沿x轴正方向运动,设运动时间为t.