题目内容
11.已知关于x、y的方程组$\left\{\begin{array}{l}{\frac{1}{3}a+\frac{2}{3}(b-x)=y}\\{b-x=y(a-1)}\end{array}\right.$的解是$\left\{{\begin{array}{l}{x=1}\\{y=2}\end{array}}\right.$,求a+b的值.分析 把$\left\{{\begin{array}{l}{x=1}\\{y=2}\end{array}}\right.$代入方程组,得出关于a,b的方程组,再解答求出a,b的值后代入a+b解答即可.
解答 解:把$\left\{{\begin{array}{l}{x=1}\\{y=2}\end{array}}\right.$代入方程组$\left\{\begin{array}{l}{\frac{1}{3}a+\frac{2}{3}(b-x)=y}\\{b-x=y(a-1)}\end{array}\right.$,
得:$\left\{\begin{array}{l}{\frac{1}{3}a+\frac{2}{3}(b-1)=2}\\{b-1=2(a-1)}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$,
把a=2,b=3代入a+b=2+3=5.
点评 此题主要考查了二元一次方程组解的定义.在求解时注意用到代入消元法.

练习册系列答案
相关题目
16.低碳生活是一项符合社会潮流的生活方式.小明的妈妈是低碳生活的响应者.他家现在用70m3水的时间和原来用90m3水的时间相同,已知原来每月比现在每月多用2m3的水.设现在小明家每月用水量为x m3,根据题意下面所列方程中正确的是( )
| A. | $\frac{90}{x+2}$=$\frac{70}{x}$ | B. | $\frac{90}{x-2}$=$\frac{70}{x}$ | C. | $\frac{90}{x}$=$\frac{70}{x+2}$ | D. | $\frac{90}{x}$=$\frac{70}{x-2}$ |
3.若$\sqrt{x-2}+|\root{3}{y}+2|=0$,则yx的值等于( )
| A. | 36 | B. | -36 | C. | 64 | D. | -64 |
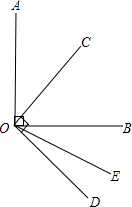 如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOE=2∠DOE,试求∠COE的度数.
如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOE=2∠DOE,试求∠COE的度数. 如图,在数学活动中,我们得知三角点阵前n行的点数之和是1+2+3+…+n(n为正整数),这个结果可用公式$\frac{1}{2}$n(n+1)求得,如果这个结果是21,那么这个三角点阵的行数n是6.
如图,在数学活动中,我们得知三角点阵前n行的点数之和是1+2+3+…+n(n为正整数),这个结果可用公式$\frac{1}{2}$n(n+1)求得,如果这个结果是21,那么这个三角点阵的行数n是6.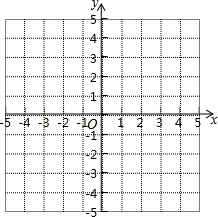 △ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).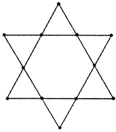 某住宅小区拟栽种12棵风景树,若想栽成6行,每行4棵,且6行树所处位置连成线后能组成精美的对称图案,请你依照举例再设计两种不同的栽树方案(不写作法)
某住宅小区拟栽种12棵风景树,若想栽成6行,每行4棵,且6行树所处位置连成线后能组成精美的对称图案,请你依照举例再设计两种不同的栽树方案(不写作法)