题目内容
4.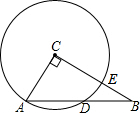 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )| A. | $\frac{18}{5}$ | B. | $\frac{5}{2}$ | C. | $\frac{24}{5}$ | D. | $\frac{9}{5}$ |
分析 先根据勾股定理求出AB的长,过C作CM⊥AB,交AB于点M,由垂径定理可知M为AD的中点,由三角形的面积可求出CM的长,在Rt△ACM中,根据勾股定理可求出AM的长,进而可得出结论.
解答 解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}{+4}^{2}}$=5, 过C作CM⊥AB,交AB于点M,如图所示,
过C作CM⊥AB,交AB于点M,如图所示,
∵CM⊥AB,
∴M为AD的中点,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CM,且AC=3,BC=4,AB=5,
∴CM=$\frac{12}{5}$,
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+($\frac{12}{5}$)2,
解得:AM=$\frac{9}{5}$,
∴AD=2AM=$\frac{18}{5}$.
故选A.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
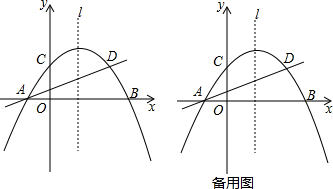
 如图,把矩形纸片OABC放在平面直角坐标系中,使OA、OC分别落在x轴正半轴、y轴正半轴上,将纸片沿AC折叠,得到点B的对应点B′.若OA=2,OC=3,则点B′的坐标为(-$\frac{10}{13}$,$\frac{15}{13}$).
如图,把矩形纸片OABC放在平面直角坐标系中,使OA、OC分别落在x轴正半轴、y轴正半轴上,将纸片沿AC折叠,得到点B的对应点B′.若OA=2,OC=3,则点B′的坐标为(-$\frac{10}{13}$,$\frac{15}{13}$).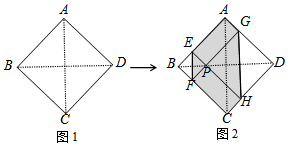 如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断: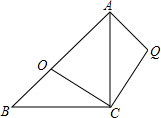 如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:$\sqrt{3}$,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=105°.
如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:$\sqrt{3}$,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=105°. 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是①②.(请写出正确结论的序号).
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是①②.(请写出正确结论的序号).