题目内容
1.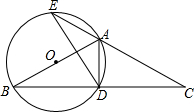 如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.(1)求证:D是BC的中点;
(2)若DE=3,BD-AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
分析 (1)根据圆周角定理求得AD⊥BC,根据等腰三角形三线合一的性质即可证得结论;
(2)先求得∠E=∠C,根据等角对等边求得BD=DC=DE=3,进而求得AD=1,然后根据勾股定理求得AB,即可求得圆的半径;
(3)根据题意得到AC=$\sqrt{10}$,BC=6,DC=3,然后根据割线定理即可求得EC,进而求得AE.
解答 (1)证明:∵AB是圆O的直径,
∴AD⊥BC,
∵AB=AC,
∴BD=DC;
(2)解:∵AB=AC,
∠B=∠C,
∵∠B=∠E,
∴∠E=∠C,
∴BD=DC=DE=3,
∵BD-AD=2,
∴AD=1,
在RT△ABD中,AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{10}$,
∴⊙O的半径为$\frac{\sqrt{10}}{2}$;
(3)解:∵AB=AC=$\sqrt{10}$,BD=DC=3,
∴BC=6,
∵∠B=∠E,∠C=∠C,
∴△EDC∽△BAC,
∵AC•EC=DC•BC,
∴$\sqrt{10}$•EC=3×6,
∴EC=$\frac{9}{5}$$\sqrt{10}$,
∴AE=EC-AC=$\frac{9}{5}$$\sqrt{10}$-$\sqrt{10}$=$\frac{4}{5}$$\sqrt{10}$.
点评 本题考查了圆周角定理,等腰三角形的判定和性质,勾股定理的应用以及割线定理的应用,熟练掌握性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下面的计算正确的是( )
| A. | 6a-5a=1 | B. | $\sqrt{36}$=±6 | C. | (a2)3=a5 | D. | 2(a+b)=2a+2b |
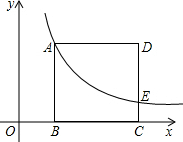 如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),则k的值为2.
如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),则k的值为2.
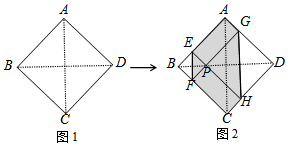 如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断: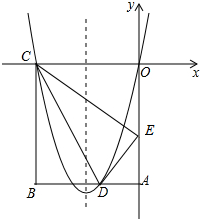 如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.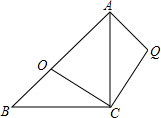 如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:$\sqrt{3}$,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=105°.
如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:$\sqrt{3}$,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=105°. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )
如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )