题目内容
10.有300个零件,由甲先独做15天,再由乙独做10天可以完成,若乙每天比甲多做5个.(1)求甲乙每天各做多少个?
(2)已知甲做一天耗资30元,乙做一天耗资50元,若工期不超过24天,为节约开支,请设计施工方案?
分析 (1)设甲每天各做x个,则乙每天各做(x+5)个,根据题意列方程,即可解答;
(2)根据甲先独做15天,再由乙独做10天可以完成和工期不超过24天列不等式组,求出乙最少做的天数,即可得到节约开支的施工方案.
解答 解:(1)设甲每天各做x个,则乙每天各做(x+5)个,根据题意列方程,
15x+10(x+5)=300
解得:x=10,
x+5=15,
答:甲乙每天分别做10个零件、15个零件.
(2)设甲做m天,乙做n天,根据题意列不等式组,
$\left\{\begin{array}{l}{m+n≤24}\\{10m+15n=300}\end{array}\right.$
解得:12≤n≤20,
因为甲做一天耗资30元,乙做一天耗资50元,所以乙做的天数越少越节省,
当n=12时,m=(300-12×15)÷10=12,
所以为节约开支,应甲、乙各做12天.
点评 本题主要考查了一元一次方程和一次不等式组的应用,正确理解数量关系和题意是解决问题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
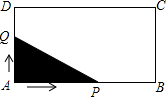 如图,长方形ABCD中,AB=4,AD=2.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为x(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的x的值或取值范围是0<x≤$\frac{4}{3}$或x=2.
如图,长方形ABCD中,AB=4,AD=2.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为x(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的x的值或取值范围是0<x≤$\frac{4}{3}$或x=2. 如图,△ABC和△DBE为等腰直角三角形,且AD=2,AE=2$\sqrt{3}$,求AC的长.
如图,△ABC和△DBE为等腰直角三角形,且AD=2,AE=2$\sqrt{3}$,求AC的长. 如图,在△ABC中,BC=10,cosC=$\frac{1}{8}$,AC=8,求∠B的正切值.
如图,在△ABC中,BC=10,cosC=$\frac{1}{8}$,AC=8,求∠B的正切值.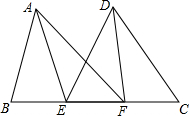 已知:点B,E,F,C在同一条直线上,AB=CD,BF=CE,AE=DF.求证:AF=DE.
已知:点B,E,F,C在同一条直线上,AB=CD,BF=CE,AE=DF.求证:AF=DE.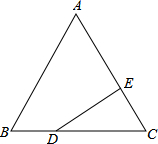 等边△ABC中,BD=$\frac{1}{3}$BC,CE=$\frac{1}{3}$AC,求证:DE⊥AC.
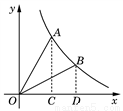
等边△ABC中,BD=$\frac{1}{3}$BC,CE=$\frac{1}{3}$AC,求证:DE⊥AC.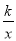 的图象经过点A(1,
的图象经过点A(1, 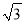 ).
).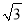 ,1)是否在此反比例函数的图象上,并说明理由.
,1)是否在此反比例函数的图象上,并说明理由.