题目内容
15．
如图，一条公路上有A，B公汽站，公路旁边的工地C处需要爆破施工，已知点C与公路上停靠站A，B之间的距离分别为300米，400米，且CA⊥CB（如图），爆破施工时，距离C处250米范围内有危险，那么公路AB段是否需要暂时封闭？为什么？
分析 如图，本题需要判断点C到AB的距离是否小于250米，如果小于则有危险，大于则没有危险．因此过C作CD⊥AB于D，然后根据勾股定理在直角三角形ABC中即可求出AB的长度，然后利用三角形的公式即可求出CD，然后和250米比较大小即可判断需要暂时封锁．
解答 
解：如图，过C作CD⊥AB于D，
∵BC=400米，AC=300米，∠ACB=90°，
∴根据勾股定理得AB=500米，
∵$\frac{1}{2}$AB•CD=$\frac{1}{2}$BC•AC，
∴CD=240米．
∵240米＜250米，故有危险，
因此AB段公路需要暂时封锁．
点评 本题考查正确运用勾股定理，善于观察题目的信息是解题以及学好数学的关键．
练习册系列答案
相关题目
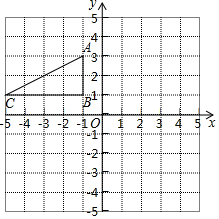△ABC在平面直角坐标系中的位置如图所示：将△ABC的横坐标不变，纵坐标乘以-1得到△A1B1C1画出图形，并说明所得的图形与原图形有什么关系？并写出A1、B1、C1的坐标．
如图：点C是线段AB上的点，点D是线段BC的中点，若AC：BC=3：2，且AD=8，求线段AB的长．