题目内容
12.小明剪了一个?ABCD,他认为∠ABC=3∠A,小亮剪了一个Rt△EFG,他认为∠FEG=90°,EF=2cm.两人对小颖说:“若拼成图①那样,则CD与GF重合;若拼成图②那样,∠BCD与∠EGF重合”两人问小颖:“在图②中,DE有多长?”你能帮小颖解答这个问题吗?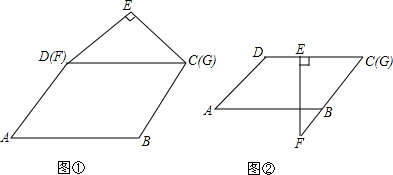
分析 根据平行四边形两邻角互补,∠ABC=3∠A,可得∠A=45°,再根据平行四边形的性质可得∠BCD的度数,根据重合可得Rt△EFG是等腰直角三角形,再根据等腰直角三角形的性质以及线段的和差关系即可得到DE有多长.
解答 解:∵四边形ABCD是平行四边形,
∴∠ABC+∠A=180°,∠A=∠BCD,
∵∠ABC=3∠A,
∴3∠A+∠A=180°,
∴∠A=45°,
∴∠BCD=45°,
∴∠EGF=45°,
∵∠FEG=90°,EF=2cm,
∴EG=2cm,CD=FG=2$\sqrt{2}$cm,
∴DE=2($\sqrt{2}$-1)cm.
故DE有2($\sqrt{2}$-1)cm长.
点评 考查了图形的剪拼,平行四边形的性质,等腰直角三角形的性质,本题关键是得到Rt△EFG是等腰直角三角形.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
2.下列方程没有实数根的是( )
| A. | x2+4x=0 | B. | x2-2x+3=0 | C. | 3x2+8x-3=0 | D. | (x-2)(x-3)=12 |
7. 如图,直线a∥b,直线c与直线a,b都相交,∠1=65°,则∠2的度数为( )
如图,直线a∥b,直线c与直线a,b都相交,∠1=65°,则∠2的度数为( )
 如图,直线a∥b,直线c与直线a,b都相交,∠1=65°,则∠2的度数为( )
如图,直线a∥b,直线c与直线a,b都相交,∠1=65°,则∠2的度数为( )| A. | 60° | B. | 125° | C. | 115° | D. | 65° |
4.一个多边形的内角和比它的外角和多了360°,这个多边形是( )
| A. | 五边形 | B. | 六边形 | C. | 七边形 | D. | 八边形 |
 如图,在正方形ABCD对角线上任意取点E,AE延长线交CD于F.交BC延长线于G.求证:EC2=EF•EG.
如图,在正方形ABCD对角线上任意取点E,AE延长线交CD于F.交BC延长线于G.求证:EC2=EF•EG.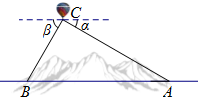 2014年11月25日,国家发改委批准了我省三条泛亚铁路的规划和建设计划.为加快勘测设计,某勘测部门使用了热气球对某隧道的长进行勘测.如图所示,热气球C的探测器显示,从热气球观测隧道入口A的俯角α为30°,观测隧道出口B的俯角β为60°,热气球相对隧道的飞行高度为1200m,求这条隧道AB的长?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留2位小数)
2014年11月25日,国家发改委批准了我省三条泛亚铁路的规划和建设计划.为加快勘测设计,某勘测部门使用了热气球对某隧道的长进行勘测.如图所示,热气球C的探测器显示,从热气球观测隧道入口A的俯角α为30°,观测隧道出口B的俯角β为60°,热气球相对隧道的飞行高度为1200m,求这条隧道AB的长?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留2位小数)