题目内容
2.计算$\underset{\underbrace{11…11}}{1999}$$\underset{\underbrace{22…22}}{1999}$÷$\underset{\underbrace{33…33}}{1999}$.分析 由12÷3=4,1122÷33=34,111222÷333=334,11112222÷3333=3334…可以看出商中3的个数是1或2的数字个数减去,末尾是4,由此规律得出答案即可.
解答 解:∵12÷3=4,
1122÷33=34,
111222÷333=334,
11112222÷3333=3334,
…
∴$\underset{\underbrace{11…11}}{1999}$$\underset{\underbrace{22…22}}{1999}$÷$\underset{\underbrace{33…33}}{1999}$=$\underset{\underbrace{333••3}}{1998}$4.
点评 此题考查因式分解的运用,数字的变化规律,找出数字之间的联系得出规律,解决问题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
12.在下列的线段a、b、c的长为三边的三角形中,不能构成直角三角形的是( )
| A. | a=9,b=41,c=40 | B. | a=b=5,c=5$\sqrt{2}$ | C. | a:b:c=3:4:5 | D. | a=11,b=12,c=15 |
11.已知a,b,c是△ABC的三边,则关于x的方程(a+b)x2-2cx+(a+b)=0的根的情况是( )
| A. | 没有实数根 | B. | 可能有且只有一个实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
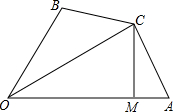 如图,在四边形OACB中,CM⊥OA于M,且CA=CB,∠OAC+∠OBC=180°,求证:
如图,在四边形OACB中,CM⊥OA于M,且CA=CB,∠OAC+∠OBC=180°,求证: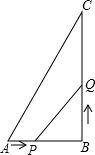 如图,Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P,Q以1cm/s的速度分别从A,B出发,点P从A到B,点Q从B到C.
如图,Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P,Q以1cm/s的速度分别从A,B出发,点P从A到B,点Q从B到C.