题目内容
(1)已知:如图(1),OA=OB,OC=OD,AD和BC相交于点P.证明:PA=PB.
(2)由(1)中的结论,你能想到不同于平时用尺规作角平分线的方法吗?试在图(2)中,用尺规作出∠MON的平分线.(保留作图痕迹,不写作法)
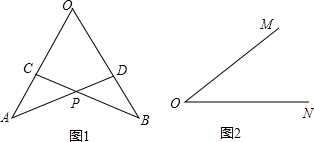
(2)由(1)中的结论,你能想到不同于平时用尺规作角平分线的方法吗?试在图(2)中,用尺规作出∠MON的平分线.(保留作图痕迹,不写作法)

考点:全等三角形的判定与性质,作图—基本作图
专题:
分析:(1)根据SAS证明△OAD≌△OBC,再由AAS证明△APC≌△BPD,从而得出PA=PB;
(2)用尺规作图法作角平分线即可.
(2)用尺规作图法作角平分线即可.
解答:证明:(1)在△OAD和△OBC中,
,
∴△OAD≌△OBC(SAS).
∴∠OAD=∠OBC.
∵OA=OB,OC=OD,
∴OA-OC=OB-OD,
即AC=BD.
∵△OAD≌△OBC,
∴∠OAD=∠OBC,
在△APC和△BPD中,
∴△APC≌△BPD(AAS).
∴PA=PB;
(2)以O为圆心,一定长为半径画弧与角两边OM、ON分别交于点A、B,再以O圆心,一定长为半径画弧与角两边OM、ON分别交于点C、D,且OC<OA.连结BC、AD交于点P,连结OP,OP即为∠MON的平分线.

|
∴△OAD≌△OBC(SAS).
∴∠OAD=∠OBC.
∵OA=OB,OC=OD,
∴OA-OC=OB-OD,
即AC=BD.
∵△OAD≌△OBC,
∴∠OAD=∠OBC,
在△APC和△BPD中,
|
∴△APC≌△BPD(AAS).
∴PA=PB;
(2)以O为圆心,一定长为半径画弧与角两边OM、ON分别交于点A、B,再以O圆心,一定长为半径画弧与角两边OM、ON分别交于点C、D,且OC<OA.连结BC、AD交于点P,连结OP,OP即为∠MON的平分线.

点评:本题考查了全等三角形的判定和性质,判断两个三角形全等的方法:SSS,SAS,ASA,AAS,还有直角三角形的判定定理:HL.

练习册系列答案
相关题目
下列说法中,不正确的是( )
| A、平方等于本身的数只有0和1 |
| B、正数的绝对值是它本身,负数的绝对值是它的相反数 |
| C、两个负数,绝对值大的负数小 |
| D、0除以任何数都得0 |
 如图,已知在平行四边形ABCD中,AE:EB=1:3.
如图,已知在平行四边形ABCD中,AE:EB=1:3. 已知在△ABC中,AD平分∠BAC,EM是AD的中垂线,交BC延长线于E,求证:DE2=BE•CE.
已知在△ABC中,AD平分∠BAC,EM是AD的中垂线,交BC延长线于E,求证:DE2=BE•CE.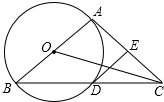 如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E,∠B=30°,求sin∠AOC=
如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E,∠B=30°,求sin∠AOC=