题目内容
已知在△ABC中，AD平分∠BAC，EM是AD的中垂线，交BC延长线于E，求证：DE2=BE•CE．考点：相似三角形的判定与性质
专题：证明题
分析：连接AE，则AE=DE，结合条件证△AEC∽△BEA，即可得到结论．
解答：
证明：
连接AE，
∵EM是AD的中垂线，
∴EA=ED，
∴∠EDA=∠EAD，
且∠EDA=∠B+∠BAD，∠EAD=∠DAC+∠CAE，
∴∠CAE=∠B，且∠AEC=∠BEA，
∴△AEC∽△BEA，
∴
=
，
∴AE2=BE•CE，
∴DE2=BE•CE．
证明：连接AE，
∵EM是AD的中垂线，
∴EA=ED，
∴∠EDA=∠EAD，
且∠EDA=∠B+∠BAD，∠EAD=∠DAC+∠CAE，
∴∠CAE=∠B，且∠AEC=∠BEA，
∴△AEC∽△BEA，
∴
| AE |
| BE |
| EC |
| AE |
∴AE2=BE•CE，
∴DE2=BE•CE．
点评：本题主要考查相似三角形的判定和性质，利用条件证明△AEC∽△BEA是解题的关键．
练习册系列答案
相关题目
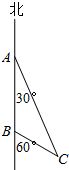如图，一条船从海岛A处向正南航行到达海岛B处，从海岛A处测得灯塔C在南偏东30°方向，从海岛B处测得灯塔C在南偏东60°方向，已知A、B两海岛距离25海里，则海岛B到灯塔C的距离为