题目内容
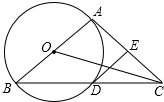 如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E,∠B=30°,求sin∠AOC=
如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E,∠B=30°,求sin∠AOC=考点:切线的性质
专题:
分析:如图,作辅助线;首先求出∠GAC=60°,分别表示出BC、CG的长度,进而求出BG、OG的长度,即可解决问题.
解答: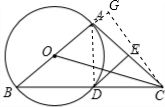 解:如图,连接AD;过点C作CG⊥BA,交BA的延长线于点G;
解:如图,连接AD;过点C作CG⊥BA,交BA的延长线于点G;
∵AB为⊙O的直径,
∴AD⊥BC,而BD=CD,
∴AB=AC,∠ACB=∠B=30°,
∴∠GAC=30°+30°=60°;
设⊙O的半径为1,则AB=2;
∴AD=1,BD=CD=
,
∴BC=2
;在直角△BCG中,
∵∠B=30°,
∴CG=
BC=
,BG=
CG=3,
∴OG=3-1=2;
由勾股定理得:OC2=4+3=7,
∴OC=
,
∴sin∠AOC=
=
,
故该题答案为
.
 解:如图,连接AD;过点C作CG⊥BA,交BA的延长线于点G;
解:如图,连接AD;过点C作CG⊥BA,交BA的延长线于点G;∵AB为⊙O的直径,
∴AD⊥BC,而BD=CD,
∴AB=AC,∠ACB=∠B=30°,
∴∠GAC=30°+30°=60°;
设⊙O的半径为1,则AB=2;
∴AD=1,BD=CD=
| 3 |
∴BC=2
| 3 |
∵∠B=30°,
∴CG=
| 1 |
| 2 |
| 3 |
| 3 |
∴OG=3-1=2;
由勾股定理得:OC2=4+3=7,
∴OC=
| 7 |
∴sin∠AOC=
| ||
|
| ||
| 7 |
故该题答案为
| ||
| 7 |
点评:该命题以圆为载体,以切线的性质、勾股定理、圆周角定理、直角三角形的边角关系等几何知识点的考查为核心构造而成;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
将6-(+3)-(-7)+(-2)写成省略加号的和的形式为( )
| A、-6-3+7-2 |
| B、6-3-7-2 |
| C、6-3+7-2 |
| D、6+3-7-2 |
 如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于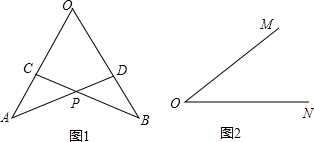
 如图,在△ABC中,CD是AB边上的中线,已知CD⊥AC,且tan∠BCD=
如图,在△ABC中,CD是AB边上的中线,已知CD⊥AC,且tan∠BCD=