题目内容
一超市销售某种品牌的牛奶，进价为每盒1.5元，售价为每盒2.2元时，每天可售5000盒，经过调查发现，若每盒降价0.1元，则可多卖2000盒．要使超市每天盈利4500元，并且使顾客得到实惠，请问该超市如何定价？
考点：一元二次方程的应用
专题：销售问题
分析：本题可设每盒子牛奶应降价x元，则每盒赢利（2.2-x-1.5）元，平均每天可售出（5000+x÷0.1×2000）盒，根据每盒的盈利×销售的盒数=销售这种牛奶的盈利，据此即可列出方程，求出答案．
解答：解：设每盒牛奶降价x元．
（2.2-1.5-x）×（5000+x÷0.1×2000）=4500
化简得：20x2-9x+1=0，即（4x-1）（5x-1）=0
解得，x1=0.2，x2=0.25﹙舍去）
∴x=0.2，
2.2-0.2=2（元）．
答：每盒牛奶应价2元．
（2.2-1.5-x）×（5000+x÷0.1×2000）=4500
化简得：20x2-9x+1=0，即（4x-1）（5x-1）=0
解得，x1=0.2，x2=0.25﹙舍去）
∴x=0.2，
2.2-0.2=2（元）．
答：每盒牛奶应价2元．
点评：考查了一元二次方程的应用，此题首先要正确理解题意，把实际问题的数量关系转化为一元二次方程求解，但应注意考虑解应符合的条件，即考虑解的取舍．
练习册系列答案
相关题目
某段河流的两岸是平行的，数学兴趣小组在老师带领下不用涉水过河就测得河的宽度，他们是这样做的：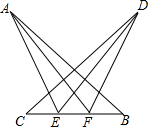
如图所示，已知AB=DC，AE=DF，CE=BF，试说明：AF=DE．