题目内容
 如图,直线交坐标轴于A(a,0),B(0,b)两点,且a,b满足a2+b2+2a-6b+10=0,AB平分∠OAC,OC交反比例函数y=-
如图,直线交坐标轴于A(a,0),B(0,b)两点,且a,b满足a2+b2+2a-6b+10=0,AB平分∠OAC,OC交反比例函数y=-| 9 |
| x |
(1)求a,b的值;
(2)求△OAC的面积.
考点:反比例函数综合题
专题:
分析:(1)根据配方,可得非负数的和为零,根据非负数的和为零,可得每个非负数为零,可得a、b得值;
(2)根据角平分线的性质,可得BD与BO的关系,根据全等三角形的判定与性质,可得AD,根据勾股定理,可得关于a、b的方程,根据解方程,可得a、b的值,根据待定系数法,可得AD的解析式,根据双曲线与AD的交点,可得C点的纵坐标,根据三角形的面积公式,可得答案.
(2)根据角平分线的性质,可得BD与BO的关系,根据全等三角形的判定与性质,可得AD,根据勾股定理,可得关于a、b的方程,根据解方程,可得a、b的值,根据待定系数法,可得AD的解析式,根据双曲线与AD的交点,可得C点的纵坐标,根据三角形的面积公式,可得答案.
解答:解:(1)a2+b2+2a-6b+10=0,配方,得
(a+1)2+(b-3)2=0.
a+1=0,b-3=0.
解得a=-1,b=3;
(2)作BD⊥AC于D,作DE⊥y轴于E点,DF⊥x轴于F点,作CG⊥x轴与G点. ,
,
设D(a,b),
由AB平分∠OAC,得
BD=BO=3,
在△DAB和△OAB中,
,
△DAB≌△OAB(HL),
∴AD=AO=1.
由勾股定理,得
,
②-①得2a+6b=0.化简,得
a=-3b③.
把a=-3b代入①,得10b2-6b=0,解得b=
,b=0(不符合题意要舍去),
把b=
代入③,得a=-
,D(-
,
),
设AD的函数解析式为y=kx+b,把A、D点的坐标代入,得
,解得
.
AD的函数解析式为y=-
x-
,
联立直线AD、反比例函数,得
,
4y2+3y-27=0
y1=
,y2=-3(不符合题意要舍去),
S△OAC=
AC•CG=
×|-1|×
=
.
(a+1)2+(b-3)2=0.
a+1=0,b-3=0.
解得a=-1,b=3;
(2)作BD⊥AC于D,作DE⊥y轴于E点,DF⊥x轴于F点,作CG⊥x轴与G点.
 ,
,设D(a,b),
由AB平分∠OAC,得
BD=BO=3,
在△DAB和△OAB中,
|
△DAB≌△OAB(HL),
∴AD=AO=1.
由勾股定理,得
|
②-①得2a+6b=0.化简,得
a=-3b③.
把a=-3b代入①,得10b2-6b=0,解得b=
| 3 |
| 5 |
把b=
| 3 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 3 |
| 5 |
设AD的函数解析式为y=kx+b,把A、D点的坐标代入,得
|
|
AD的函数解析式为y=-
| 3 |
| 4 |
| 3 |
| 4 |
联立直线AD、反比例函数,得
|
4y2+3y-27=0
y1=
| 9 |
| 4 |
S△OAC=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 8 |
点评:本题考查了反比例函数综合题,(1)利用了非负数的性质,(2)利用了角平分线的性质,全等三角形的判定与性质,勾股定理,函数图象交点与方程组的关系,三角形的面积公式.

练习册系列答案
相关题目
计算:(2+1)(22+1)(24+1)(28+1)的值为( )
| A、48-1 |
| B、264-1 |
| C、26-1 |
| D、23-1 |
 如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,若AB=CD=4,则梯形ABCD的周长为( )
如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,若AB=CD=4,则梯形ABCD的周长为( )| A、16 | ||
| B、18 | ||
| C、20 | ||
D、12+4
|
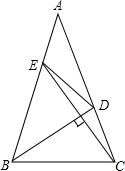 如图,△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,CE⊥BD交于E,连接DE,则图中等腰三角形有( )
如图,△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,CE⊥BD交于E,连接DE,则图中等腰三角形有( )| A、3个 | B、4个 | C、5个 | D、6个 |
正六边形的每个内角为( )
| A、120° | B、135° |
| C、140° | D、144° |
 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).