题目内容
18.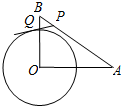 如图,在Rt△OAB中,∠AOB=90°,OA=8,AB=10,⊙O的半径为4.点P是AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x(0≤x≤10),PQ2=y,则y与x的函数关系式为y=x2-$\frac{64}{5}$x+48.
如图,在Rt△OAB中,∠AOB=90°,OA=8,AB=10,⊙O的半径为4.点P是AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x(0≤x≤10),PQ2=y,则y与x的函数关系式为y=x2-$\frac{64}{5}$x+48.
分析 连接OQ、OP、作PM⊥OA于M,由PM∥BO,得$\frac{PM}{BO}$=$\frac{AM}{AO}$=$\frac{PA}{AB}$,求出PM、AM,利用OP2=PQ2+OQ2=PM2+OM2,列出等式即可解决问题.
解答 解: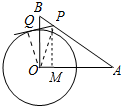 如图连接OQ、OP、作PM⊥OA于M.
如图连接OQ、OP、作PM⊥OA于M.
∵PQ是⊙O切线,
∴∠PMA=∠BOA=90°,AO=8,AB=10,
∴PM∥BO,BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=6,
∴$\frac{PM}{BO}$=$\frac{AM}{AO}$=$\frac{PA}{AB}$,
∴PM=$\frac{3}{5}$x,AM=$\frac{4}{5}$x.OM=8-$\frac{4}{5}$x,
∵OP2=PQ2+OQ2=PM2+OM2,
∴y+16=$\frac{9}{25}$x2+64-$\frac{64}{5}$x+$\frac{16}{25}$x2,
∴y=x2-$\frac{64}{5}$x+48,
故答案为y=x2-$\frac{64}{5}$x+48
点评 本题考查切线的性质、平行线分线段成比例定理、勾股定理等知识,解题的关键是添加辅助线构造直角三角形,利用勾股定理建立函数关系,属于中考常考题型.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
6.$-\frac{1}{4}$的相反数是( )
| A. | $-\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -4 | D. | 4 |
13.据深圳特区报3月30日早间消息,华为公司获得2016中国质量领域最高奖.华为公司将2016年销售收入目标定为818亿美元,是国内互联网巨头BAT三家2014年收入的两倍以上.其中818亿美元可用科学记数法表示为( )美元.
| A. | 8.18×109 | B. | 8.18×1010 | C. | 8.18×1011 | D. | 0.818×1011 |
3.某校七年级各班分别选出3名学生组成班级代表队,参加知识竞赛,得分最多的班级为优胜班级,各代表队比赛结果如下:
(1)写出表格中得分的众数、中位数;
(2)学校从获胜班级的代表队中各抽取1名学生组成“绿色环保监督”小组,小明、小红分别是七(4)班和七(6)班代表队的学生,用列表法或画树状图的方法说明同时抽到小明和小红的概率是多少?
| 班级 | 七(1) | 七(2) | 七(3) | 七(4) | 七(5) | 七(6) | 七(7) | 七(8) | 七(9) | 七(10) |
| 得分 | 85 | 90 | 90 | 100 | 80 | 100 | 90 | 80 | 85 | 90 |
(2)学校从获胜班级的代表队中各抽取1名学生组成“绿色环保监督”小组,小明、小红分别是七(4)班和七(6)班代表队的学生,用列表法或画树状图的方法说明同时抽到小明和小红的概率是多少?