题目内容
8.(1)用12个除颜色外其他都相同的球,设计一个摸球游戏,使摸到红球的概率为$\frac{1}{2}$,摸到黄球的概率为$\frac{1}{3}$(2)如果要使摸到红球的概率为$\frac{2}{3}$,摸到黄球的概率为$\frac{1}{6}$,那么摸球游戏至少要设置几个球?
分析 (1)根据概率的计算公式求解即可;
(2)借助概率的计算公式设计即可.
解答 解:(1)∵12个小球,6个红球,4个黄球,2个白球
∴P(摸到红球)=$\frac{6}{12}$=$\frac{1}{2}$,P(摸到黄球)=$\frac{4}{12}$=$\frac{1}{3}$
(2)∵3和6的最小公倍数是6.
∴6个小球,4个红球,1个黄球,一个白球,
∴P(摸到红球)=$\frac{4}{6}$=$\frac{2}{3}$,P(摸到黄球)=$\frac{1}{6}$.
点评 此题是概率公式题,主要考查了概率的计算公式的应用,解本题的关键是掌握公式的前提下,能灵活运用.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
13.$\sqrt{2x-3}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥$\frac{3}{2}$ | B. | x>$\frac{3}{2}$ | C. | x≤$\frac{3}{2}$ | D. | x<$\frac{3}{2}$ |
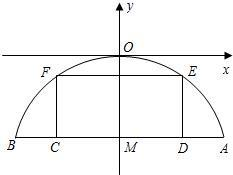 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
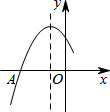 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论: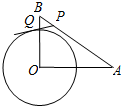 如图,在Rt△OAB中,∠AOB=90°,OA=8,AB=10,⊙O的半径为4.点P是AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x(0≤x≤10),PQ2=y,则y与x的函数关系式为y=x2-$\frac{64}{5}$x+48.
如图,在Rt△OAB中,∠AOB=90°,OA=8,AB=10,⊙O的半径为4.点P是AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x(0≤x≤10),PQ2=y,则y与x的函数关系式为y=x2-$\frac{64}{5}$x+48.