题目内容
9.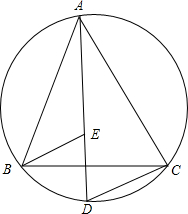 如图,△ABC的顶点A,B,C都在圆上,$\widehat{AB}$=$\widehat{BC}$=$\widehat{AC}$,D是$\widehat{BC}$上一点,连接AD,在AD上截取AE=DC,试判断△BDE的形状,并说明理由.
如图,△ABC的顶点A,B,C都在圆上,$\widehat{AB}$=$\widehat{BC}$=$\widehat{AC}$,D是$\widehat{BC}$上一点,连接AD,在AD上截取AE=DC,试判断△BDE的形状,并说明理由.
分析 根据圆心角、弧、弦的关系,由$\widehat{AB}$=$\widehat{BC}$=$\widehat{AC}$得到AB=BC=AC,则可判断△ABC为等边三角形,则∠ACB=60°,再证明△ABE≌△CBD得到BE=BD,接着根据圆周角定理得到∠ADB=∠ACB=60°,于是可判断△BDE为等边三角形.
解答 解:△BDE为等边三角形.理由如下:
∵$\widehat{AB}$=$\widehat{BC}$=$\widehat{AC}$,
∴AB=BC=AC,
∴△ABC为等边三角形,
∴∠ACB=60°,
在△ABE和△CBD中,
$\left\{\begin{array}{l}{AB=CB}\\{∠BAE=∠BCD}\\{AE=CD}\end{array}\right.$,
∴△ABE≌△CBD,
∴BE=BD,
∵∠ADB=∠ACB=60°,
∴△BDE为等边三角形.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了全等三角形的判定与性质和等边三角形的判定.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
20.下列计算正确的是( )
| A. | 2x+3y=5xy | B. | x2•x3=x6 | C. | (a3)2=a6 | D. | (ab)3=ab3 |
17.下列美丽图案,是轴对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.某班一次数学小测验中,共出了20道选择题和填空题,总分为100分,现从中抽出5份试卷进行分析,如表:
(1)某同学得了70分,他答对了多少道题?
(2)有一同学H说他得了86分,另一同学G说他得72分,谁说得对?
| 试卷 | 正确个数 | 错误个数 | 得分 |
| A | 19 | 1 | 94 |
| B | 18 | 2 | 88 |
| C | 17 | 3 | 82 |
| D | 14 | 6 | 64 |
| E | 10 | 10 | 40 |
(2)有一同学H说他得了86分,另一同学G说他得72分,谁说得对?
 已知如图在△ABC中,AB=AC,AD⊥AB,BD=7,AD=3.5,则∠BAC=120°;CD=3.5.
已知如图在△ABC中,AB=AC,AD⊥AB,BD=7,AD=3.5,则∠BAC=120°;CD=3.5. 如图,在△ABC中,AD⊥BC于D,点M、N分别在BC所在的直线上,且AB=AC,BM=CN,试判断△AMN的形状,并说明理由.
如图,在△ABC中,AD⊥BC于D,点M、N分别在BC所在的直线上,且AB=AC,BM=CN,试判断△AMN的形状,并说明理由. 如图,在△ABC中,∠B=90°,AB=9cm,点P从点A开始沿AB方向以1cm/s的速度移动,点Q从点B开始沿BC方向以2cm/s的速度移动,如果点P,Q分别从点A,B同时出发,几秒后△PQB为等腰三角形?
如图,在△ABC中,∠B=90°,AB=9cm,点P从点A开始沿AB方向以1cm/s的速度移动,点Q从点B开始沿BC方向以2cm/s的速度移动,如果点P,Q分别从点A,B同时出发,几秒后△PQB为等腰三角形?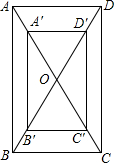 一个矩形的广告牌如图所示,印刷厂的纸张的印刷面积是32dm2,上、下空白各1dm,左、右空白处各0.5dm,被印刷部分从上到下的长是xdm,四周空白处的面积为Sdm2.
一个矩形的广告牌如图所示,印刷厂的纸张的印刷面积是32dm2,上、下空白各1dm,左、右空白处各0.5dm,被印刷部分从上到下的长是xdm,四周空白处的面积为Sdm2.